Теория припекания порошковых слоев в двухпараметрическрй модели вязко пористой среды
§ 2. Метод вычисления средних по объему.
Рассмотрим метод вычисления по объему порошкового слоя, значение его величины 
в соответствии с [5]. Причем выражено она будет через усредненные по объему параметры вязкости порошковой системы, внешние силы, приложенные к границам слоя, и геометрические параметры границ.
Имеем по определению:
(1)
Интеграл в (1) взят по всему объему V пористой среды. С другой стороны у нас
(2)
Поэтому выражение (1) приводится к виду
(3)
Здесь 
- среднее значение функции 
в объеме пористого слоя.
Запишем граничные условия в виде:
(4)
где 
- компонента единичного вектора внешней нормали в декартовых координатах х1, х2, х3, а 
- компоненты внешней силы, отнесенные к единице площади граничной поверхности 
.
Введем в рассмотрение тензор 3-го ранга:
(5)
В силу обобщенной теоремы Гаусса-Остроградского, имеем:
(6)
Здесь вектор площадки 
на границе можно представить согласно
(7)
С другой стороны, имеем для интеграла слева в (6) выражение, вытекающее из определения:
(8)
Как и в [5] примем сначала, что можно пренебречь силами инерции в слое, а также предположим, что нет массовых сил:
.
Тогда имеем уравнение равновесия слоя:
(9)
и
(10)
Это уравнение получено посредством (6) и (8).
Подставляя этот результат в (3), получаем, положив 
:
(11)
Таким образом, среднее значение величины
выражено через кинетическую константу
процессов в компактном материале слоя, усредненную функцию пористости , внешние силы 
и геометрические параметры границы.
§ 3. Кинетика припекания слоя в жесткой пресс-форме.
Внешнее давление приложено вдоль оси OZ.
, все 
, кроме 
. (12)
Далее имеем
(13)
Вычисляем поверхностный интеграл, учитывая граничные условия в (13)
(14)
При вычислении (14) заменили средне по области границ значение величины 
на 
. Подставляя результат (14) в (11), получим:
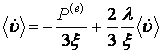(15)
Отсюда следует кинетическое уравнение припекания:
(16)
В дальнейшем будем опираться на это уравнение.
Если проинтегрировать (16) при 
, то получим
(17)
Использовались соотношения:
(18)
(19)
(20)
(21)
ГЛАВА II. ТЕОРИЯ ПРОЦЕССОВ ПРИПЕКАНИЯ С ПОСТОЯННОЙ СКОРОСТЬЮ НАГРЕВА СЛОЯ.
§ 1. Спекание с 
Используя материал главы I, рассмотрим процессы припекания в условиях переменной температуры.
Положим
(1)
Тогда уравнение (16) главы I с учетом соотношений (18-21) примет вид:
(2)
Здесь
(3)
причем,
, 
, 
(4)
Функция пористости имеет вид:
Перейти на страницу: 1 2 3 4 5 6