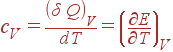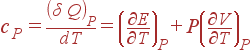Очевидно, что величина теплоемкости зависит от того, нагревается ли тело при постоянном объеме или при постоянном давлении ::: physicedu.ru

Первое начало термодинамики

Страница 2

Очевидно, что величина теплоемкости зависит от того, нагревается ли тело при постоянном объеме или при постоянном давлении. Обозначим символами cV и cP теплоемкости при постоянном объеме и при постоянном давлении соответственно. Поскольку при V = const, dV = 0, то

$c_V=\frac{\left( \delta Q\right) _V}{dT}=\left( \frac{\partial E}{\partial T}\right) _V$

(9)

Подобным же образом из (8) получается выражение для cP:

$c_P=\frac{\left( \delta Q\right) _P}{dT}=\left( \frac{\partial E}{\partial T}\right) _P+P\left( \frac{\partial V}{\partial T}\right) _P$

(10)

Второй член в формуле для cP связан со слагаемым PdV, т.е. описывает эффеккт, оказываемый на теплоемкость работой, которую система совершает во время расширения. В (9) подобного члена нет, поскольку объем остается постоянным и работа не совершается. (1)

Во многих случаях удобно пользоваться понятием молярной теплоемкости. Молярной теплоемкостью называется теплоемкость одного моля вещества. Молярные теплоемкости при постоянном V и при постоянном P определяются формулами (9) и (10), если вместо произвольного количества вещества взять 1 моль:

$C_V=\left( \frac{\partial \widetilde{E}}{\partial T}\right) _V , C_P=\left( \frac{\partial \widetilde{E}}{\partial T}\right) _P+P\left( \frac{\partial \widetilde{V}}{\partial T}\right)_P ,$

(11)

знак $\widetilde{}$ сверху означает, что взят 1 моль вещества. (2)

В случае газа можно конкретизировать зависимость внутренней энергии E от переменных T и V, определяющих его состояние. В дальнейшем мы докажем, что энергия идеального газа определяется температурой T и не зависит от объема V: E = E(T). Для реальных газов это утверждение выполняется приближенно. Для определения зависимости E(T) воспользуемся результатами опыта, согласно которым теплоемкость газов очень слабо зависит от температуры. Можно предположить, что для идеального газа она строго постоянна. Тогда интегрирование уравнения

$C_V=\left( \frac{\partial \widetilde{E}}{\partial T}\right) _V=\frac{d\widetilde{E}}{dT}$

(12)

при условии CV = const дает:

$\widetilde{E}=C_VT+E_0 ,$

(13)

где E0– константа, представляющая энергию газа при абсолютном нуле. Внутренняя энергия N молей газа

E = N(CVT+E0) .

(14)

Для идеального газа 1-й закон термодинамики принимает вид

$\delta \widetilde{Q}=C_VdT+P d\widetilde{V} .$

(15)

Из этого уравнения легко получить соотношение между молярными теплоемкостями CV и CP. Для этого перейдем от переменных T и V к переменным T и P. Это можно сделать, если взять дифференциалы от обеих частей уравнения состояния для 1 моля идеального газа

$P\widetilde{V}=RT ,$

(16)

что дает

$P d\widetilde{V}+\widetilde{V} dP=R dT .$

Выражая отсюда $Pd\widetilde{V}$ и подставляя в (15), получаем

$\delta \widetilde{Q}=C_VdT+R dT-\widetilde{V} dP .$

Отсюда можно легко найти CP. Поскольку при P = const дифференциал dP = 0 , то

$C_P=\frac{\left( \delta \widetilde{Q}\right) _P}{dT}=C_V+R ,$

(17)

т.е. разность между молярными теплоемкостями газа при постоянном давлении и при постоянном объеме равна газовой постоянной R . (1)

Литература: 1.Мякишев Г.Я., Буховцев Б.Б. Физика 10 кл. 2.Шахмаев Н.М. Физика 10 кл. 3.Свитков Л.П. Термодинамика и молекулярная физика 1970г. 4.Билимович Б.Ф. Тепловые явления в технике1981г.

Перейти на страницу: 1 2

Первое начало термодинамики

Разделы