Торричелли
Предположим, что искомая точка М лежит вне треугольника и расположена так, как указано на рис. 2а.
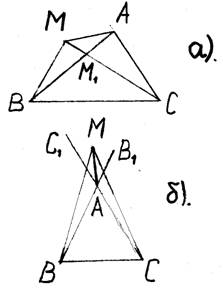
Рис. 2
Тогда МА + МВ + МС не может быть наименьшим, так как М1А + М1В + М1С < МА´ + МВ + + МС (где М1 – точка пересечения прямой МС со стороной АВ). Пусть точка М расположена так, как указано на рис. 9б, то есть точка М расположена внутри угла В1АС1. В этом случае МВ +МС > АВ + АС (объемлющая более объемлемой), а поэтому МА +МВ + МС > АВ + АС.
Итак, точка, сумма расстояний которой до вершин треугольника имеет наименьшее значение, лежит либо внутри треугольника, либо совпадает с одной из его вершин.
Перейдем непосредственно к решению задачи о нахождении точки Торричелли.
Пусть Р – произвольная точка внутри треугольника АВС.
Найдем сумму отрезков РА+РВ+РС. (Рис. 3)
Повернем ∆ВРА на угол в 60° вокруг точки В так, чтобы он оказался вне треугольника АВС. Точка А займет положение А1, не зависящее от выбора точки Р.
Точка Р займет положение Р1.
∆РВР1 – равносторонний: РР1 = РВ
РА + РВ + РС = А1Р1 + Р1Р + РС.
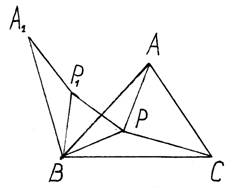
Рис. 3
Наименьшее значение будет для точки Р, лежащей на прямой А1С. Так как в этом случае Р1, Р, С лежат на одной прямой, то угол ВРС, смежный с углом равностороннего треугольника, равен 120°; т. к. угол А1Р1В, равный 120°, равен АВС, то и угол АРВ = 120°.
Итак, для отыскания точки Р строим на каждой из сторон сегмент, вмещающий угол в 120°. Точка пересечения дуг сегментов – искомая точка.
Точка Р находится внутри треугольника, если среди углов нет угла, равного или большего 120°.
Рассмотрим случаи: а) когда один из углов ∆АВС равен 120°;
б) когда один из углов ∆АВС больше 120°.
а) В плоскости ∆АВС с углом А = 120° найдем точку Торричелли.
○ Построив равносторонние ∆АСВ1 и ∆АВС1, докажем, что вершина А – искомая точка. Покажем, что для всякой точки, лежащей внутри треугольника, например для точки Р, имеет место соотношение РА + РВ + РС > АВ +АС. (Рис.4.)

Рис. 4.
Построим на отрезке АР равносторонний треугольник АРР1. Из равенства ∆В1Р1А = ∆СРА (АВ1 = АС; АР1=АР; ÐРАС=ÐВ1АР1) следует, что РС = Р1В1.
Итак:
РА + РВ + РС = РВ + РР1 + Р1В;
РВ + РР1 + Р1В1 > В1В;
РВ + РА + РС > АВ + АС.●
б) В плоскости ∆АВС с углом А > 120° найдем точку Торричелли.
Покажем, что искомой точкой является вершина тупого угла.
Возьмем произвольную точку Р внутри треугольника и покажем, что сумма РА + РВ + РС > АВ + АС. (Рис.5.)
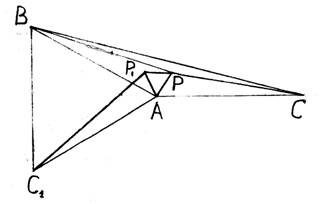
Рис. 5
Построим равносторонние треугольники РАР1 и АВС1.
∆АВР = ∆АР1С1 (АР = АР1;
АВ = АС1; ÐРАВ = ÐР1АС1).
Следовательно ВР=Р1С1; поэтому
РС + РА + РВ = РС +РР1 + Р1С1
и далее
РА + РВ + РС > АС + АС1;
РА + РВ + РС > АС +АВ.
Задача о нахождении точки Торричелли решена.
Литература.
1. Радемахер Г., Тенлиц О. Числа и фигуры. – М.: Физматгиз, 1962. – С. 22 – 29.
2. Болтянский В. Г., Яглом И. М. Геометрические задачи на максимум и минимум//Энциклопедия элементарной математики. Т. V. – М.: Наука, 1966
3. Брокгауз Ф_А_, Ефрон И_А_ Энциклопедический словарь -Москва Высшая Школа 1986.
Перейти на страницу: 1 2
