Исследование системы возбуждения электроразрядного эксимерного лазера выполненной по типу LC-инвертора
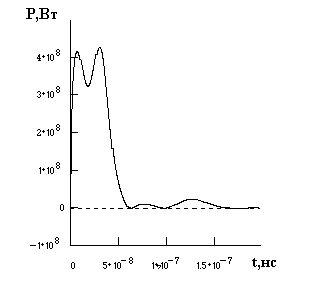
На рис.12 и рис.13 представлены зависимости от времени мощности энерговклада. В первом случае, как видно из рис.12, процесс передачи энергии в активную среду происходит практически в течении первых 50-60 нс. В последующие моменты времени энерговклад в межэлектродный промежуток весьма незначителен. Благодаря обострительной емкости наблюдается два всплеска кривой мощности энерговклада, причем во втором случае данный эффект проявляется ярче из-за большего значения обострительной емкости. Второй случай характеризуется так же тем, что длительность процесса энерговклада значительно увеличивается и составляет 100-120 нс.
 |
 |
Таким образом, с помощью созданной математической модели схемы накачки, выполненной по типу LС-инвертора, появилась возможность получать и анализировать зависимости от времени такие характеристики электрической схемы накачки, как токи, протекающие через элементы схемы (в том числе и через разрядный промежуток) , напряжения на элементах схемы, а также общий энерговклад в активную среду и мощность энерговклада.
3. Теоретическое исследование электроразрядного эксимерного лазера с возбуждением схемы выполненной по типу LC-инвертора
3.1 Исследование зависимости энерговклада
от сопротивления разрядного промежутка
В процессе расчетов параметров схемы LC-инвертора сопротивление разрядного промежутка моделировалось функцией зависимости сопротивления от времени, таким образом, что за время порядка 20-50 нс. сопротивление разрядного промежутка изменялось от 5 Ом до 0.3 Ом. Данная функция имеет следующий вид:
![]()
Возможность применения данной функции обусловлена экспериментальными данными, представленными в работах [11],[10] . Легко видеть, что в нашем случае сопротивление разрядного промежутка будет зависеть от трех параметров: Rn (начальное значение сопротивления R2), R0 (конечное значение сопротивления R2) и параметр а, характеризующий скорость падения сопротивления.
В данном параграфе рассмотрим влияние данных параметров на величину вкладываемой в разрядный промежуток энергиии.
На рис.16 представлена зависимость вложенной энергии от конечного значения сопротивления разрядного промежутка. Значения сопротивления варьировались в пределах от 0.01Ом до 1 Ом.
Из рис.16 видно, что при значениях сопротивления порядка 0.2-0.3 Ом кривая зависимости энерговклада от конечного значения сопротивления имеет пологий максимум. При дальнейшем увеличении сопротивления энерговклад весьма незначительно уменьшается. Таким образом, изменение конечного значения сопротивления в пределах 0.2-0.8 Ом не приводит к значительному изменению значения вложенной в межэлектродный промежуток энергии. Следовательно, приняв, что конечное значение сопротивления равняется 0.3 Ом, мы не вносим существенной погрешности в дальнейшие вычислении.
 |
Рис.18 Зависимость энерговклада от конечного значения сопротивления разрядного промежутка 1)C1=C2=50, 2)C1=C2=150,C1=C2=200 нф.
 |
Рис.17 Зависимость энерговклада от параметра а, 1)L1=17 нГн , 2)L2=70 нГн.
Физический смысл параметра а заключается в том, что величина t=1/а есть время, за которое сопротивление разрядного промежутка уменьшается в е раз. Данная величина зависит от многих факторов: наличия определенного числа первоначальных электронов предионизации, давления, состава рабочей смеси т. д
. Из рис.17 видно, что с ростом параметра а (и с уменьшением t) энерговклад растет и при достижении а=2*108 кривая зависимости выходит на насыщение и далее на значение вложенной в межэлектродный промежуток энергии не оказывает какого-либо существенного влияния. Это значение параметра а и будем в дальнейшем использовать в вычислениях, не рискуя внести существенную погрешность в дальнейший ход расчетов.
Величина начального значентя сопротивления может быть выбрана достаточно произвольно, так как она зависит от соотношения параметров Rn и а.В началный момент времени сопротивление разрядного промежутка должно иметь достаточно большое значение (бесконечность). В нашем случае примем, что начальное значение сопротивления межэлектродного промежутка равняется 5 Ом.
На рис.18 представлена зависимость сопротивления разрядного промежутка от времени с учетом выбранных выше оптимальных значений параметров данного сопротивления.
Рис.18. Зависимость от времени сопротивления разрядного промежутка.
Таким образом, проведенный анализ показал, что выбранная функция, модулирующая динамику изменения со временем сопротивления разрядного промежутка, может с достаточно большой точностью использоваться при дальнейших расчетах.
2.5 Исследование зависимости энерговклада от параметров элементов цепи возбуждения
В общем случае LC-инвертор содержит шесть контуров. Исследовать экспериментально динамику процессов выделения энергии на элементах цепи возбуждения, в том числе и на сопротивлении разрядной плазмы в межэлектродном промежутке достаточно сложно. Исследуем зависимости вложенной в разрядный промежуток энергии от параметров элементов схемы возбуждения с помощью полученной модели, и сравним полученные теоретические данные с экспериментальными, представленными в работах [10,11].
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10
