Построение волновых функций для атома и молекулы, используя пакет аналитических вычислений Maple
 СФЕРИЧЕСКАЯ ФОРМА s-орбитали
СФЕРИЧЕСКАЯ ФОРМА s-орбитали
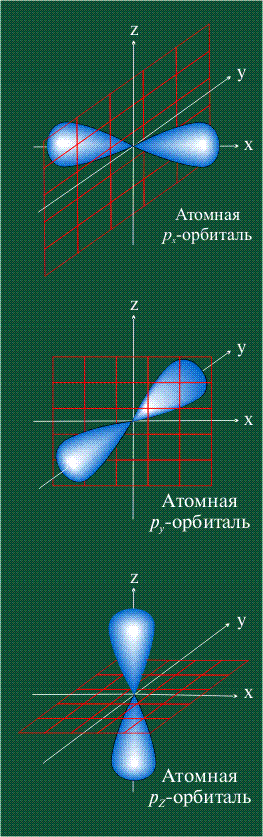 РАСПОЛОЖЕНИЕ В ПРОСТРАНСТВЕ р-орбиталей
РАСПОЛОЖЕНИЕ В ПРОСТРАНСТВЕ р-орбиталей
 ФОРМЫ d-ОРБИТАЛЕЙ
ФОРМЫ d-ОРБИТАЛЕЙ
 ФОРМЫ f-ОРБИТАЛЕЙ
ФОРМЫ f-ОРБИТАЛЕЙ
 ФОРМА g-ОРБИТАЛИ
ФОРМА g-ОРБИТАЛИ
Гибридизация атомных орбиталей. Молекулярные орбитали. По методу молекулярных орбиталей любая молекула рассматривается как совокупность всех ядер и электронов всех атомов, образующих данную сложную частицу. Существует несколько вариантов этого метода. Рассмотрим один из них, наиболее распространённый. ЛКАО МО - линейная комбинация атомных орбиталей - есть молекулярная орбиталь.
Образование её можно представить как результат сложения и вычитания комбинируемых атомных орбиталей. Если атомные орбитали обозначить φA и φB, то их линейная комбинация даст молекулярные орбитали двух типов. При сложении возникает молекулярная орбиталь ψ+, при вычитании - ψ-.
Сложение означает, что молекулярная орбиталь характеризуется повышенной электронной плотностью в пространстве между ядрами, поэтому энегетически она выгоднее исходных атомных орбиталей. Такая орбиталь называется связующей.
При вычитании атомных орбиталей образуется орбиталь с пространственным разрывом между ядрами. Электронная плотность равна нулю, и подобная орбиталь энергетически менее выгодна, чем исходные атомные орбитали. Такая молекулярная орбиталь называется разрыхляющей.

 ГИБРИДИЗАЦИЯ с участием двух орбиталей, s и px
ГИБРИДИЗАЦИЯ с участием двух орбиталей, s и px
 ГИБРИДИЗАЦИЯ с участием трех орбиталей: s, px и py
ГИБРИДИЗАЦИЯ с участием трех орбиталей: s, px и py
|
Описание движения в кулоновском поле (сферические координаты), используя Maple. Рассмотрим атом водорода в квантовой механике. Напомним, что при движении в центрально-симметричном поле момент количества движения сохраняется. В силу этого, в волновой функции можно выделить радиальную и угловую часть. Наиболее прямой способ вычисления собственных функций момента движения есть непосредственное решение об отыскании собственных функций квадрата момента, записанного в сферических координатах. При этом, собственные функции момента оказываются ничем иным, как определенным образом нормированными сферическими функциями. В данном примере мы графически представим собственные функции стационарных состояний и обсудим некоторые их свойства. Итак, нам известно, что полная волновая функция ![]() =
= ![]() разлагается на три части и, поэтому, рассмотрим эти части отдельно. Угловая часть волновой функции Собственная функция третьей проекции оператора момента равна
разлагается на три части и, поэтому, рассмотрим эти части отдельно. Угловая часть волновой функции Собственная функция третьей проекции оператора момента равна ![Phi[m] = 1/sqrt(2*Pi)](images/referats/217/image034.gif)
 . В обозначениях Maple это выглядит следующим образом > restart: > Phi:=(2*Pi)^(-1/2)*exp(I*m*phi);
. В обозначениях Maple это выглядит следующим образом > restart: > Phi:=(2*Pi)^(-1/2)*exp(I*m*phi);






