Дросселирование пара
Температура идеального газа в результате дросселирования не изменяется, и эффект Джоуля-Томсона в данном случае равен нулю. Таким образом, изменение температуры реального газа при дросселировании определяется величиной отклонения свойств реального газа от идеального, что связано с действием межмолекулярных сил. Доставка цветов в Катав-Ивановске благоухающие цветы среди-цветов.ру.
Предположим, что р1v1 = p2v2 и, следовательно, u2=u1. Так как v2 > v1 , то при дросселировании внутренняя потенциальная энергия газа возрастает, а внутренняя кинетическая энергия при этом уменьшается. Следовательно, при принятых условиях температура газа после дросселирования будет уменьшаться.
Обычно при дросселировании реального газа p1v1 – p2v2 >0 и u2 – u1>0, работа проталкивания газа приводит к росту внутренней энергии.
В условиях, когда работа проталкивания оказывается больше прироста внутренней потенциальной энергии ∆uпот , ее избыток идет на увеличение и внутренней кинетической энергии ∆uкин , температура газа растет (dT>0). Когда работа проталкивания меньше ∆uпот, то ∆uкин уменьшается, температура газа понижается (dT<0). При равенстве работы проталкивания и изменения внутренней потенциальной энергии температура газа остается неизменной (dT=0).
Различают дифференциальный и интегральный температурные дроссель-эффекты. При дифференциальном эффекте Джоуля-Томсона температура изменяется на бесконечно малую величину, а при интегральном - на конечную величину. Если давление газа уменьшается на бесконечно малую величину dp, то происходит бесконечно малое изменение температуры, т.е. dTi=aidpiили
ai =(¶T/¶p)i . (5)
Величина ai, называется дифференциальным температурным эффектом Джоуля-Томсона. Значение ai, можно определить из уравнения
di = cpdT-[T(¶v/¶T)p-v]dp. (6)
Учитывая, что при дросселировании нет изменения энтальпии (di = 0), получим
СpdT= [T(¶v/¶T)p -v]dp. (7)
Отсюда
ai =(¶T/¶p)i = [T(¶v/¶T)p - v]/cp. (8)
Полагая, что реальный газ является Ван-дер-Ваальсовским газом, из уравнения (p + a/v2 )(v - b)=RT получим
T = (pv + a/v-ab/ v2 -pb)/R.(9)
После преобразований получаем:
![]() (10)
(10)
Таким образом, по уравнениям (9) и (10) можно определить значения ai при заданном давлении р1. Для этого, задаваясь различными значениями удельного объема v, по (9) вычисляют соответствующие им температуры, затем, подставляя v и Т в (10) значение дифференциального дроссель-эффекта (dT/dp)h.
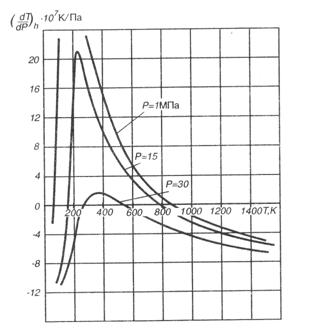
В качестве примера на рис.4 приведены зависимости дифференциального эффекта дросселирования воздуха от температуры T1 при различных давлениях р1 построенные в соответствии с результами вычислений по уравнениям (9) и (10) при критических параметрах воздуха Tкр =132,46 K, pкр =3,7 Мпа; теплоемкости cp =1015 Дж/(кг·К); газовой постоянной R=287 Дж/(кг·К) и численных значениях коэффициентов а=164,78 Н·м4/кг2, b=1,28·10-3 м3/кг
Дроссельный эффект может быть положительным, отрицательным или равным нулю. Положительный дроссель-эффект имеет место в случае, когда при дросселировании температура газа понижается. Отрицательный – когда повышается. В случае неизменности температуры при дросселировании
|
наблюдается нулевой эффект Джоуля-Томсона. Состояние реального газа при дросселировании, когда дроссельный эффект равен нулю, называется точкой инверсии. В этой точке происходит смена знака температурного эффекта. Если температура газа перед дросселированием меньше температуры инверсии, то газ при дросселировании охлаждается, если больше - то нагревается.
Для нахождения условий, при которых происходит изменение температуры газа или она остается неизменной, необходимо проанализировать уравнение
dT= {[T(¶v/¶T)p - v]/cp}dp (11)
При дросселировании dp< 0, так как давление газа всегда уменьшается. Теплоемкость ср - величина положительная. Отсюда следует, что знак dTзависит от знака выражения T(¶v/¶T)p–v и всегда ему противоположен. Тогда
приT(¶v/¶T)p–v>0dT<0,
при T(¶v/¶T)p–v<0 dT>0,
при T(¶v/¶T)p–v=0 dT=0,
Случай, когда dT = 0 можно использовать для получения температуры инверсии Tин .
T(¶v/¶T)p –v =0 Þ Tин= v/(¶v/¶T)p (12)
Последнее выражение называется уравнением кривой инверсии. Перенеся значения температур инверсии при различных давлениях в pT-координаты, получим кривую 1 инверсии (рис. 5), в каждой точке которой дроссель-эффект равен нулю и температура газа при дросселировании не изменяется. Точки на поле
|
