Космические скорости. Движение планет и спутников
Рассмотрим движение тела, брошенного на расстоянии h от поверхности Земли, с начальной скоростью 
в горизонтальном направлении при отсутствии взаимодействия с атмосферой Земли.
С момента начала движения тело будет двигаться с ускорением 
свободного падения, скорость тела будет изменяться по направлению и модулю. При небольших значениях начальной скорости траектория движения тела пересекается с поверхностью Земли. Чем больше начальная скорость движения тела, тем дальше от начальной точки оно достигает поверхности Земли. Определим, при каком значении начальной точки тело, брошенное горизонтально, будет настолько же удаляться от Земли при движении по инерции, насколько будет приближаться в результате свободного падения.
Работа от прямых работодателеи в самаре работа в самаре от прямых работодателей.
Первая космическая скорость
Для осуществления равномерного движения по окружности радиуса r его горизонтально направленная скорость должна иметь такое значение 
, при котором центростремительное ускорение равно ускорению свободного падения
(1).
Из (1) следует:
(2).
Скорость , при которой тело может двигаться по круговой орбите вокруг Земли, называется первой космической скоростью.
Из формулы (2) для значения r, равного радиусу Земли, r
6371 км, первая космическая скорость равна
м/с
При начальной скорости меньше 7,9 км/с тело, брошенное горизонтально, пролетев некоторое расстояние, упадет на поверхность Земли. При скорости 7,9 км/с в отсутствии воздуха оно будет двигаться вокруг Земли по окружности, став ее искусственным спутником.
Вторая космическая скорость
При небольшом превышении первой космической скорости орбита спутника будет эллиптической, а при достижении скорости 11,2 км/с превращается в параболу, ветви которой уходят в бесконечность.
Скорость, при которой тело способно преодолеть действия сил притяжения небесного тела и удалиться от него на бесконечно далекое расстояние, называется второй космической скоростью.
Из формулы (2) следует, что для вычисления первой космической скорости на расстоянии r от любого небесного тела, звезды или планеты, нужно знать ускорения a свободного падения на этом расстоянии от центра масс небесного тела. Небесное тело массой M действует на другое тело массой m на расстоянии r силой всемирного тяготения F.
Следовательно, ускорение свободного падения тела на этом расстоянии равно
(3).
Из (2) и (3) первая космическая скорость на расстоянии r от центра небесного тела массой M равна:
(4).
Формула (4) позволяет вычислять массы небесных тел, вокруг которых обращаются другие небесные тела под действием сил всемирного тяготения.
Массу M Солнца можно найти по известным значениям скорости движениям Земли по ее орбите и радиусу r земной орбиты:
Скорость движения Земли по орбите можно найти, зная радиус r земной орбиты и период Т ее обращения вокруг Солнца:
Для вычисления массы Солнца получаем формулу:
(5).
Выразим период обращения Земли вокруг Солнца в единицах СИ:
с
Подставим числовые значения величин, найдем массу Солнца:
кг
Из формулы (5) следует, что для всех спутников, обращающихся по круговым орбитам вокруг одной планеты, или для всех планет, обращающихся вокруг одной звезды, отношение квадратов периодов обращения к кубам радиусов орбит является величиной одинаковой
(6).
Равенство (6) выполняется и в случае движения спутников или планет по эллиптическим орбитам, если использовать как r большие полуоси эллипсов.
Третий закон Кеплера
Факт, что квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их эллиптических орбит, был открыт Иоганном Кеплером и называется третьим законом Кеплера:
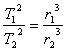(7).
Перейти на страницу: 1