Влияние вращательного и поступательного движения молекул на теплоёмкость многоатомных газов
![]()
![]()
![]()
Благодаря большой величине моментов инерции многоатомных молекул (и соответственно малости их вращательных квантов) их вращение можно всегда рассматривать классически[1]. Многоатомная молекула обладает тремя вращательными степенями свободы и тремя в общем случае различными главными моментами инерции I1, I2, I3; поэтому ее кинетическая энергия вращения есть
![]()
где x, h, z — координаты вращающейся системы, оси которой совпадают с главными осями инерции молекулы, (оставляем пока в стороне особый случай молекул, составленных из атомов, расположенных на одной прямой). Это выражение должно быть подставлено в статистический интеграл
 (2.1)
(2.1)
где
![]()
а штрих у интеграла означает, что интегрирование должно производиться лишь по тем ориентациям молекулы, которые физически отличны друг от друга.
Если молекула обладает какими-либо осями симметрии, то повороты вокруг этих осей совмещают молекулу саму с собой и сводятся к перестановке одинаковых атомов. Ясно, что число физически неразличимых ориентации молекулы равно числу допускаемых ею различных поворотов вокруг осей симметрии (включая тождественное преобразование—поворот на 360°). Обозначив это число посредством s [2] , можно производить интегрирование в (2.1) просто по всем ориентациям, одновременно разделив все выражение на s. В произведении djxdjhdjz (трех бесконечно малых углов поворота) можно рассматривать djx, djh, как элемент dsz телесного угла для направлений оси z.
Интегрирование по dsz производится независимо от интегрирования по поворотам djz вокруг самой оси z и дает 4p. После этого интегрирование по djz дает еще 2p.
Интегрируя также и по dMxdMhdMz (в пределах от -¥ до +¥), найдем в результате
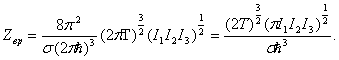
Отсюда свободная энергия

Таким образом, для вращательной теплоемкости имеем в соответствии с (1.3)
![]()
а химическая постоянная

Если все атомы в молекуле расположены на одной прямой (линейная молекула), то она обладает, как и двухатомная молекула, всего двумя вращательными степенями свободы и одним моментом инерции /. Вращательные теплоемкость и химическая постоянная равны, как и у двухатомного газа,
![]()
![]()
где s=1 для несимметричной молекулы (например, NNO) и s=2 для молекулы, симметричной относительно своей середины (например, ОСО).
Колебания молекул.
Колебательная часть термодинамических величин газа становится существенной при значительно более высоких температурах, чем вращательная, потому что интервалы колебательной структуры термов велики по сравнению с интервалами вращательной структуры.
Мы будем считать, однако, температуру большой лишь настолько, чтобы были возбуждены в основном не слишком высокие колебательные уровни. Тогда колебания являются малыми (а потому и гармоническими), и уровни энергии определяются обычным выражением ħw(u + 1/2).
Число колебательных степеней свободы определяет число так называемых нормальных колебаний молекулы, каждому из которых соответствует своя частота wa (индекс a нумерует нормальные колебания). Надо иметь в виду, что некоторые из частот wa могут совпадать друг с другом; в таких случаях говорят о кратной частоте.
Вычисление колебательной статистической суммы Zкол производится элементарно. Вследствие очень быстрой сходимости ряда суммирование можно формально распространить до u=¥. Условимся отсчитывать энергию молекулы от наиболее низкого (u = 0) колебательного уровня, т. е. включаем ħw/2 в постоянную e0 в
![]()
В гармоническом приближении, когда мы считаем колебания малыми все нормальные колебания независимы, и колебательная энергия есть сумма энергий каждого колебания в отдельности. Поэтому колебательная статистическая сумма
![]() ,
,
распадается на произведение статистических сумм отдельных колебаний,

а для свободной энергии FKOJl получается сумма выражений
![]() ,
,
т. е.

В эту сумму каждая частота входит в числе раз, равном ее кратности. Такого же рода суммы получаются соответственно для колебательных частей других термодинамических величин.
Каждое из нормальных колебаний дает в своем классическом предельном случае (T>>ħwa) вклад в теплоемкость, равный c(a)кол = 1 при Т, большем наибольшего из ħwa , получилось бы скол = rкол . Фактически, однако, этот предел не достигается, так как многоатомные молекулы обычно распадаются при значительно более низких температурах.
Различные частоты wa многоатомной молекулы разбросаны обычно в очень широком интервале значений. По мере повышения температуры постепенно «включаются» в теплоемкость различные нормальные колебания. Это обстоятельство приводит к тому, что теплоемкость многоатомных газов в довольно широких интервалах температуры часто можно считать примерно постоянной.
Перейти на страницу: 1 2 3 4 5
