Связанные контура
Максимальные значения вторичного тока I2 при связи, больше вторичной критической, наблюдаются на частотах связи w01 и w02, при которых Х1=0. Для того чтобы найти условия возникновения частот связи и определить их значения, (11) и (13) нужно представить в явной относительно частоты форме и исследовать (13) на экстремум, т. е. установить, при каких относительных расстройках (e) вторичный ток будет максимальным и минимальным. Чтобы получить выражения для I1 и I2 в явной относительно частоты форме, перепишем (11), подставив вместо Z1э его значение из (8)
Считая, что контуры настроены в резонанс (w1 = w2= w0), вынесем за скобки в знаменателе w0L и, подставив на основании (2) 
получим
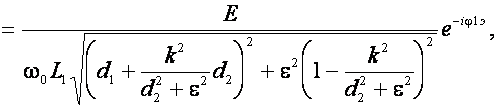(15)
где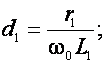 
, 
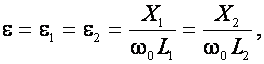
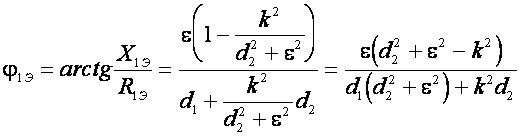. (16)
Модуль тока 
равен
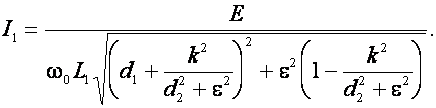(17)
Подставив в (7) вместо М. его значение из (2) и домножив числитель и знаменатель (7) на w0 L2 , найдем,
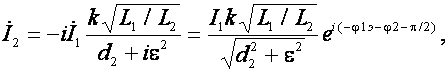(18)
где 
. Выражения (13) и (18) — идентичны. Взяв модуль (18) и подставив значение модуля I1 из (17), получим
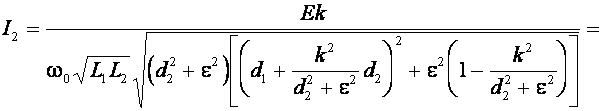
(19)
Если частота питающего генератора равна резонансной частоте контуров, т. е. wг = w0 (e = 0), то (19) упрощается
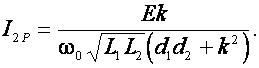
В относительных единицах выражение, описывающее резонансную кривую для тока I 2, имеет вид
(20)
Выражения (17) и (19) соответствуют (12) и (14) и описывают амплитудно-резонансные характеристики токов I1 и I2 в явной относительно частоты (расстройки e) форме.
Исследуем (19) на экстремум, для чего продифференцируем (19) по e и приравняем производную нулю, т. е. dI 2 /de = 0. В результате получим 
. Данное уравнение имеет три корня:
(21)
При d1 = d2 получаем
(22)
Если первый корень (e1) действителен при любых соотношениях между k и d, то второй и третий корни (e2 и e3) имеют смысл только при k > d. При k<d подкоренное выражение будет мнимым и физического смысла не имеет. В этом случае физический смысл имеет только первый корень (e1), что говорит об одногорбости резонансной характеристики для I2. При k > d физический смысл имеют все три корня, что говорит о двугорбом характере резонансной характеристики для тока I2. Очевидно, вторичный критический коэффициент связи, лежащий на границе перехода от одногорбой кривой к двугорбой, на основании (21) получается тогда, когда корни (21) обращаются в нуль: 
При d1 = d2 имеем:
k кр2 = d. (23)
Чтобы получить выражения для частот связи при k > kкр2, в (22) надо подставить значение e = а/Q = 1 — w02/w2. Тогда
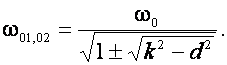(24)
Именно на частотах w01 и w02 выполняется условие резонанса, благодаря чему ток /а достигает максимума (рис. 5, б).
Третья резонансная частота получается из условия e1 =0, или e1=1- w02/w2=0; отсюда w = w0. При k > kкр2 на частоте w0 резонансная характеристика тока I2 имеет впадину. При k < kкр2, когда физический смысл имеет только первый корень , системе связанных контуров свойственна лишь одна резонансная частота w0 на которой наблюдается максимум тока I2 (рис.5, а). Наличие одной резонансной частоты при k<kкр и появление частот связи при k>kкр хорошо иллюстрирует рис. 6.
Фазово-частотные резонансные характеристики системы двух связанных контуров представляют собой частотную зависимость фазового сдвига между токами 
и приложенной к системе э. д. с. Е. Как следует из (11), сдвиг фазы между током и э. д. с. Е зависит от угла -j1э, значение которого определяется (16). Сдвиг фазы между током 
и э. д. с. Е зависит от угла 
[см. (18) ] и отличается от сдвига фазы между током и э.д.с. Е углом 
. Фазово-частотные характеристики системы двух связанных контуров изображены на рис. 7.
Полоса пропускания системы двух связанных контуров.
В одиночном контуре относительная расстройка e = 2Dw/wо = 1/Q = d. Полоса пропускания системы может быть как меньше полосы пропускания одиночного контура (при k < kкр), так и больше ее (при k³ kкр). Самой широкой полосой пропускания системы двух связанных контуров будет такая, в пределах которой провал амплитудно-частотной резонансной характеристики системы лежит на уровне 1/
от максимального значения; при этом e=2Dw/w0 » 3.1d а коэффициент связи, обеспечивающий данную полосу, k=2.41d. Как видно, при этом полоса пропускания системы двух связанных контуров в три раза шире полосы пропускания одиночного колебательного контура. При критической связи (k = kкр= d), обеспечивающей наибольшее приближение резонансной характеристики в пределах полосы пропускания к прямоугольнику, e= 1,41d.
Перейти на страницу: 1 2 3 4 5