Рефераты по Физике

Теплопроводность через сферическую оболочку

Страница 3

. (2.11)

Вектор плотности теплового потока направлен по нормали к изотермической поверхности в сторону убывания температуры. Векторы j и grad T лежат на одной прямой, но направлены в противоположные стороны.

Тепловой поток q, прошедший сквозь произвольную поверхность S, находят из выражения

. (2.12)

Количество теплоты, прошедшее через эту поверхность в течение времени t, определяется интегралом

. (2.13)

Таким образом, для определения количества теплоты, проходящего через какую-либо произвольную поверхность твердого тела, необходимо знать температурное поле внутри рассматриваемого тела. Нахождение температурного поля и составляет основную задачу аналитической теории теплопроводности. 2.4 Дифференциальное уравнение теплопроводности

Изучение любого физического процесса связано с установлением зависимости между величинами, характеризующими данный процесс. Для сложных процессов, к которым относится передача теплоты теплопроводностью, при установлении зависимостей между величинами удобно воспользоваться методами математической физики, которая рассматривает протекание процесса не во всем изучаемом пространстве, а в элементарном объеме вещества в течение бесконечно малого отрезка времени. Связь между величинами, участвующими в передаче теплоты теплопроводностью, устанавливается дифференциальным уравнением теплопроводности. В пределах выбранного элементарного объема и бесконечно малого отрезка времени становится возможным пренебречь изменением некоторых величин, характеризующих процесс.

При выводе дифференциального уравнения теплопроводности принимаются следующие допущения:

· внутренние источники теплоты отсутствуют;

· среда, в которой распространяется тепло, однородна и изотропна;

· используется закон сохранения энергии, который для данного случая формулируется так: разность между количеством теплоты, вошедшей вследствие теплопроводности в элементарный параллелепипед за время dt и вышедшей из него за тоже время, расходуется на изменение внутренней энергии рассматриваемого элементарного объема.

Выделим в среде элементарный параллелепипед с ребрами (рисунок 2.2). Температуры граней различны, поэтому через параллелепипед проходит теплота в направлении осей . Через площадку за время dt, согласно уравнению Фурье, проходит количество теплоты:

(2.14)

(grad T взят в виде частной производной, т.к. предполагается зависимость температуры не только от x, но и от других координат и времени).

Через противоположную грань на расстоянии dz отводится количество теплоты, определяемое из выражения:

, (2.15)

где — температура второй грани, а величина определяет изменение температуры в направлении z.

Рисунок 2.2

Последнее уравнение можно представить в другом виде:

. (2.16)

Итак,приращение внутренней энергии в параллелепипеде за счёт потока тепла в направлении оси z равно:

. (2.17)

Приращение внутренней энергии в параллелепипеде за счёт потока тепла в направлении оси y выразится аналогичным уравнением:

, (2.18)

а в направлении оси x:

. (2.19)

Полное приращение внутренней энергии в параллелепипеде:

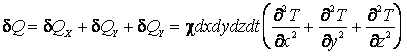. (2.20)

С другой стороны, согласно закону сохранения энергии:

, (2.21)

где — объем параллелепипеда;

— масса параллелепипеда;

c — удельная теплоемкость среды;

— плотность среды;

— изменение температуры в данной точке среды за время dt.

Левые части уравнения (2.20) и (2.21) равны, поэтому:

, (2.22)

или

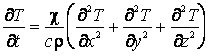. (2.23)

Величину называют оператором Лапласа и обычно обозначают сокращенно ; величину называют температуропроводностью и обозначают буквой a. При указанных обозначениях дифференциальное уравнение теплопроводности принимает вид:

Перейти на страницу:  1  2  3  4  5