Электрон в потенциальной яме. Туннельный эффект
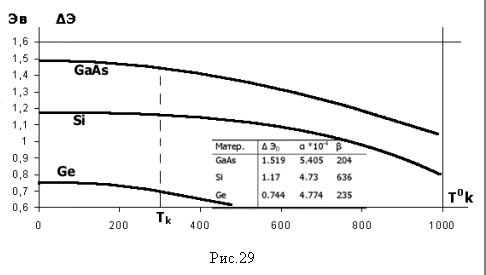
При комнатной температуре ширина DЭ увеличивается с ростом давления: в Ge d(DЭ)/dP=5*10-6 эВ/(кг/см2), а в GaAs d(DЭ)/dP ~ 12.6*10-6 эВ/(кг/см2).
В кремнии ширина DЭ с ростом давления уменьшается (d( )/dP=-2.4*10-6 эВ/(кг/см2)).
Однако энергию, необходимую для перевода электрона в свободное состояние или для образования дырки, может дать не только тепловое движение, но и другие источники энергии: энергия света, поток заряженных частиц, энергия поля, механическая энергия и т.д.
Электрические свойства определяются условиями взаимодействия и расстояниями между атомами вещества и не являются непременной особенностью данного атома (углерод в виде алмаза - диэлектрик, в виде графита - проводник).
Энергетические зоны примесей и дефектов
Примеси и дефекты нарушают строгую периодичность структуры и создают особые энергетические уровни, которые располагаются в запрещенной зоне идеального кристалла.
Если примесные атомы и дефекты расположены достаточно далеко друг от друга, то взаимодействие между ними отсутствует, а соответствующие им энергетические уровни оказываются дискретными. Поскольку туннельные переходы электронов между удаленными примесными атомами практически невозможны, то дополнительные электронные состояния локализованы в определенном месте решетки, т.е. на дефекте структуры. При достаточно высокой концентрации примесных атомов расстояния между ними сравнимы с размерами атомов, благодаря чему возможно перекрытие электронных оболочек ближайших атомов примеси. В этом случае дискретные энергетические уровни примесей расщепляются в энергетическую зону примесных состояний, способную обеспечить проводимость, если не все уровни в этой зоне заполнены электронами.
Таким образом, электрические свойства твердых тел определяются теоретически с единой точки зрения - энергия возбуждения носителей заряда или энергия активации электропроводности равна нулю у металлов и непрерывно возрастает в ряду полупроводников, условно переходящих при увеличении этой энергии в ряд диэлектриков.
Следует подчеркнуть, что зонная теория строго применима к твердым телам с ковалентными и металлическими связями.
Разделение твердых тел на полупроводники и диэлектрики носит в значительной мере условный характер.
ТУННЕЛЬНЫЙ ЭФФЕКТ
Введение
70 лет назад наш соотечественник Г. А. Гамов впервые получил решения уравнения Шредингера, описывающие возможность преодоления частицей энергетического барьера даже в случае, когда энергия частицы меньше высоты барьера. Новое явление, называемое туннелированием, позволило объяснить многие экспериментально наблюдавшиеся процессы. Найденное решение позволило понять большой круг явлений и было применено для описания процессов, происходящих при вылете частицы из ядра, - основы атомной науки и техники. Многие считают, что за грандиозность результатов его работ, ставших основополагающими для многих наук, Г. А. Гамов должен был быть удостоен нескольких Нобелевских премий. Развитие электроники подошло к использованию процессов туннелирования лишь почти 30 лет спустя: появились туннельные диоды, открытые японским ученым Л. Есаки, удостоенным за это открытие Нобелевской премии. Еще через 5 лет Ю. С. Тиходеев, руководивший сектором физико-теоретических исследований в московском НИИ "Пульсар", предложил первые расчеты параметров и варианты использования приборов на основе многослойных туннельных структур, позволяющих достичь рекордных по быстродействию результатов. Спустя 20 лет они были успешно реализованы. В настоящее время процессы туннелирования легли в основу технологий, позволяющих оперировать со сверхмалыми величинами порядка нанометров (1нанометр=10-9 м). [1]
1. Теория туннельного эффекта
Туннельный эффект — квантовое явление проникновения микрочастицы из одной классически доступной области движения в другую, отделённую от первой потенциальным барьером (рис.1.1).[2]. Если рассматривается микрообъект, например, электрон в потенциальной яме, то в отличие от классической механики существует конечная вероятность обнаружить этот объект в запрещенной области пространства, там, где его полная энергия меньше, чем потенциальная энергия в этой точке.[3] Вероятность обнаружения частицы в какой-либо точке пространства пропорциональна квадрату модуля волновой функции Y. При подлёте к потенциальному барьеру частица пройдёт сквозь него лишь с какой-то долей вероятности, а с какой-то долей вероятности отразится. Коэффициент туннелирования (прохождения, просачивания) частицы через барьер D равен:
D=e(-2a/ ћ)(2m(U0-E))½ (1)
где а – ширина барьера, U0 – высота барьера.
Главная особенность (1) заключается в том, что очень малая величина ћ (постоянная Планка) стоит в знаменателе экспоненты, вследствие чего коэффициент туннелирование через барьер классической частицы большой массы очень мал.[4] Чем меньше масса частицы, тем больше и вероятность туннельного эффекта. Так, при высоте барьера в 2 эВ и ширине 10‑8 см вероятность прохождения сквозь барьер для электрона с энергией 1 эВ равна 0,78, а для протона с той же энергией лишь 3,6×10-19 . Если же взять макроскопическое тело — шарик массой в 1 г, движущийся по горизонтальной поверхности с очень малой скоростью (кинетическая энергия близка к нулю), то вероятность преодоления им препятствия — лезвия бритвы толщиной 0,1 мм, выступающего над горизонтальной поверхностью на 0,1 мм, равна 10-26.
Прохождение частицы сквозь потенциальный барьер можно пояснить и с помощью соотношения неопределённостей. Неопределённость импульса D р на отрезке D х, равном ширине барьера а, составляет: Dр > ћ/а. Связанная с этим разбросом в значениях импульса кинетическая энергия (Dр)2/2m0 может оказаться достаточной для того, чтобы полная энергия частицы оказалась больше потенциальной. [2].
3.Туннельный эффект в физике
Перейти на страницу: 1 2 3 4 5
