Исследование систем возбуждения эксимерных лазеров на основе LC-контура
Ниже в разделах 1.1-1.2 приведены результаты исследования выходных генерационных характеристик XeCl-лазера с возбуждением LC-контуром при изменении его параметров в широком диапазоне [5-13]. Эти исследования позволяют определить оптимальные параметры системы возбуждения для достижения максимальной энергии, мощности и КПД генерации, получения гладкого временного профиля импульса, а также сформулировать критерии, по которым можно целенаправленно управлять характеристиками генерации эксимерных лазеров.
Целью настоящего этапа являлось экспериментальное и теоретическое установление оптимальных условий возбуждения электроразрядных эксимерных лазеров.
1. Исследование систем возбуждения эксимерных лазеров
на основе LC-контура
1.1. Компьютерное моделирование систем возбуждения эксимерных лазеров на основе LC-контура
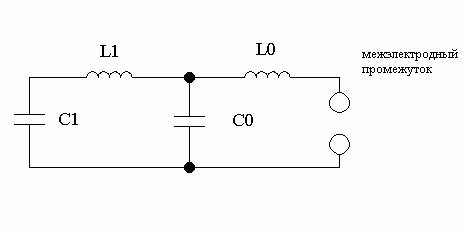
Как система возбуждения лазера, LC-контур содержит накопительную емкость С1 и последовательно включенную с ней через индуктивность L1 обострительную емкость C0 (см. рис.1,а). Так как С1 перезаряжается на С0 через коммутатор, который обладает активным сопротивлением, сравнимым с сопротивлением плазмы в межэлектродном промежутке, то на нем теряется
значительная часть энергии, запасенной в С1. Следовательно, одним из путей увеличения эффективности и выходной энергии генерации является уменьшение потерь на коммутаторе. Возможны следующие характерные режимы работы LC-контура.
1. При малых величинах обострительной емкости С0 её основная функция состоит в формировании объемного разряда. Она заряжается от накопительной емкости С1 до напряжения порядка двойного зарядного, а затем быстро разряжается на межэлектродный промежуток. При столь высоком перенапряжении (>5 кВ/(см атм.) и крутом фронте импульса возбуждения формируется однородный объемный разряд. Сама обострительная емкость С0 разряжается на стадии пробоя, когда сопротивление разрядной плазмы достаточно высоко. Основной энерговклад в разряд в этом случае осуществляется от накопительной емкости С1.
2. При увеличением обострительной емкости С0 (при одновременном увеличении L1) ее роль изменяется. Наряду с формированием разряда она осуществляет и энерговклад в разряд. Причем его мощность сравнима с мощностью энерговклада от С1.
3. Если величина обострительной емкости С0 становится одного порядка с накопительной С1, то возможен режим работы с полной перезарядкой. В
LC-контур
 |
б
 |
С1, С0 – накопительная и обострительная емкости; L1 и L0 – контурные индуктивности; Сe - межэлектродная емкость; R(t) –сопротивление междуэлектродного промежутка; LS – собственная индуктивность разряда; I1, I2, Ir– токи через соответствующие элементы; U1 – напряжение на емкости C1; U0– напряжение на емкости C0; Ue – разность потенциалов на емкости Ce; U – напряжение на лазерных электродах; Rk – сопротивление разрядников.
Рис.1
этом случае вся энергия запасенная в С1 переходит в обостритель С0, причем именно в таком режиме обеспечивается как правило максимальный К.П.Д. лазера [14].
Нами была создана компьютерная программа расчета холостого и рабочего режимов работы системы возбуждения на основе LC-контура. По расчетной схеме на рис.1,б была составлена следующая система уравнений:
(1)
гдеI1, I2, Ir– токи через соответствующие элементы (рис.1,б); U1 – напряжение на емкости C1; U0– напряжение на емкости C0; Ue – разность потенциалов на емкости Ce; U – напряжение на лазерных электродах; Rk – сопротивление разрядников.
В расчетной схеме (рис.1,б) введена межэлектродная емкость Ce, сопротивление разряда R(t) и собственная индуктивность разряда LS. Эти три величины моделируют импеданс разряда. Напряженность электрического поля 
в разряде имеет две составляющие.
(2)
Первое слагаемое в (2) является напряженностью электростатического поля, обусловленного зарядами. Второе слагаемое вызвано переменным магнитым полем. В квазистационарном прибижении вектор потенциал 
определяется токами протекающими в системе, поэтому второе слагамое зависит от скорости изменения токов и можно записать
(3)
Зависимость сопротивления разряда от времени задавалась в следующем виде
(4)
Такая зависимость сопротивления разряда от времени получается в случае, если плотность электронов n удовлетворяет следующему уравнению.
(5)
Где 
– эффективная частота ионизации; β – коэффициент рекомбинации. Решение уравнения (5) при начальном условии n(0)=np(начальная концентрация электронов, то есть созданная предыонизацией) имеет следующий вид
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10