Исследование систем возбуждения эксимерных лазеров на основе LC-контура
(6)
где - 
стационарная концентрация электронов, достигаемая за достаточно большой промежуток времени. Эффективная частота ионизации зависит от ионизационного коэффициента α и дрейфовой скорости электронов Vd следующим образом.
(7)
Представим ионизационный коэффициент a в форме Таунсенда.
(8)
Дрейфовую скорость электронов в следующем виде.
(9)
Тогда на основании выражений (7-8) имеем
(10)
Где Р – давление газа. То есть, в общем случае (при μР
const) частота ионизации зависит от давления газа Р и отношения Е/P. Поэтому, при получении решения уравнения (5) в форме (6), подразумевалось, что величины Р и Е/P постоянны. Удельное сопротивление плазмы ρ равно
(11)
На основании (6 и 11) имеем
(12)
где 
- начальное удельное сопротивление (соответствует концентрации электронов np ; 
- стационарное удельное спротивление (соответствует концентрации электронов 
). Тогда в выражении (4)
; (13)
(14)
где l расстояние между электродами; S площадь, занимаемая разрядом на электроде. Таким образом выражение (4) строго выполняется только при постоянном Е/P. Однако, оно успешно применятся для аппроксимации разрядного сопротивления. Это связано с тем, что сопротивлении разрядной плазмы очень быстро ~ 20 нс выходит на некоторый практически постоянный уровень. На этом уровне скорость ионизационные процессы практически равна нулю (первый член в правой части уравнения (5) обращается в ноль) и происходит медленная рекомбинация плазмы по уравнению
(15)
Решение этого уравнения при начальном условии n(0)=n0 имеет вид
(16)
На основании (11-16) сопротивление разрядного промежутка меняется медленно по закону
(17)
Этим изменением мы пренебрегаем.При расчетах величина R1 бралась в пределах 2-10 кОм; R0 ~ 0.1 Ом; a ~ (1
100)x107, Rk ~ (0,11) Ом в зависимости от числа используемых разрядников. При этом обеспечивалось наилучшее совпадение экспериментальных и расчетных осциллограмм. На рис.2-6 представлены расчетные осциллограммы напряжения U(t) на межэлектродном промежутке и мощности P(t) энерговклада в разряд, полученные в результате численного решения системы уравнений (1) при помощи стандартных программ MathCard 7. Расчетные осциллограммы (рис.2-7) будут проанализированы детально при обсуждении экспериментальных данных, полученных при тех же параметрах системы возбуждения. На рис.6 показана зависимость мощности энерговклада от времени при двух разных значениях сопротивления коммутатора Rk Уменьшение сопротивления Rk в целом спосоствует росту мощности энерговклада. На рис.7 предаставлены осциллограммы импульсов напряжения(U) и разности потенциалов (Ue) на разрядном промежутке. Они получены при разных L0 и LS, но L0+LS=const. При этом импульс напряжения на разряде не меняется, а импульс разность потенциалов меняется. На практике, при использовании делителя напряжения мы
Расчетные осциллограммы
 |
 |
а - L1=11 нГн; б – L1=23 нГн;
С1=75 нФ; С0=3,6 нФ; U0=40 кВ; Rk=0,3 Ом; L0=5 нГн; LS=1 нГн
Рис.2
Расчетные осциллограммы
 |
 |
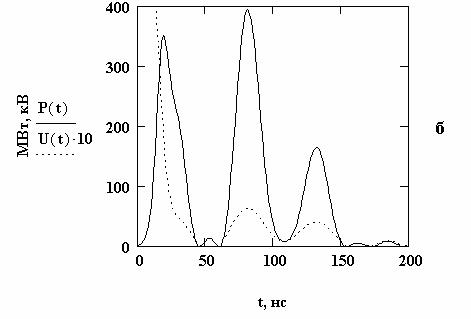а - L1=11 нГн; б – L1=23 нГн;
С1=75 нФ; С0=15 нФ; U0=40 кВ; Rk=0,3 Ом; L0=5 нГн; LS=1 нГн
Рис.3
Расчетные осциллограммы
 |
 |
а - L1=11 нГн; б – L1=23 нГн;
С1=75 нФ; С0=37 нФ; U0=40 кВ; Rk=0,3 Ом; L0=5 нГн; LS=1 нГн
Рис.4
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10