Математическое моделирование физических задач на ЭВМ
(3.2)
Строка матрицы А показывает, какие ветви выходят из каждого независимого узла графа цепи (и входят в него), а столбец – к каким узлам присоединена ветвь.
В отличие от полной матрицы Аа у редуцированной матрицы соединений связного графа множество всех строк линейно независимо. Отсюда можно сделать вывод о том, что система уравнений равновесия токов в ny-1 узлах цепи линейно независима. Если ввести вектор токов пв, ветвей:
i=[i1, i2, … inв]Т, (3.3)
то систему независимых уравнений в nу-1 узлах по ЗТК в соответствии со смыслом матрицы А можно записать в виде:
Ai=0, (3.4)
где 0=[0 0 … 0]T - нулевой вектор размерности nу-1.
Для графа цепи рис. 3.1, б с матрицей соединений (3.2) имеем:
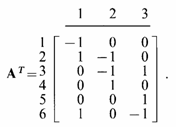
Транспонированная матрица соединений имеет вид:
(3.5)
Строка этой матрицы показывает, между какими узлами присоединена каждая ветвь.
Если задана матрица соединений, то всегда можно построить соответствующий граф. Для этого, расположив точки, обозначающие узлы, следует соединить их попарно ветвями. Номера и направление ветвей определяются ненулевыми элементами столбцов матрицы соединения.
2. Уравнения контурных токов
Метод контурных токов применим к цепям с планарным графом (рис. 3.3, а). В качестве переменных принимают замкнутые контурные токи, проходящие по ветвям, образующим все внутренние ячейки графа.
Если намечать контуры – периметры ячеек – по порядку, начиная с одного края цепи, то легко убедиться, что в каждый последующий контур вносится новая ветвь, не вошедшая в предыдущие контуры. Отсюда следует, что уравнения равновесия напряжений в таких контурах будут линейно независимы. Число внутренних ячеек равно nx=nв-ny+1.
Каждой ячейке приписывается один контурный ток, замыкающийся по ветвям, образующим ячейку. Общее число переменных – контурных токов – равно числу ячеек. Направления всех контурных токов принимают одинаковыми – по часовой стрелке. Как видно из рис. 3.3, a, по каждой ветви цепи, за исключением периферийных ветвей, замыкаются два контурных тока, направленные в противоположные стороны. Запишем уравнения соединений.
1. Приравнивая нулю суммы напряжений ветвей всех независимых контуров (ячеек), имеем nх уравнений по ЗНК 
.
2. Выражая ток каждой ветви через разность двух (в общем случае) замыкающихся по смежным контурам контурных токов, получим nв уравнений по ЗТК:
.
Как видно, токи всех ветвей, т. е. поведение всей цепи, полностью определяются nх контурными токами, число которых меньше числа ветвей.
Запишем уравнения ветвей. Положим для удобства, что выполнено преобразование всех источников тока и цепь содержит только источники напряжения. Примем для общности каждую ветвь состоящей из последовательного соединения резистивного элемента и источника напряжения (рис. 3.3,6). Уравнение такой составной ветви имеет вид:
.
Для получения уравнений относительно выбранных переменных необходимо:
1) с помощью уравнений ветвей в уравнениях равновесия напряжений заменить напряжения всех ветвей токами;
2) токи ветвей в получившейся системе заменить, согласно , контурными токами.
Получим уравнения для одной из ячеек, например первой (рис. 3.3, в), образованной тремя ветвями. Основным уравнением равновесия напряжений в первом контуре будет:
u1+u2+u3=0 (*)
Токи ветвей ячейки:
.(**)
Уравнения ветвей:
(***)
Из трех систем уравнений (*), (**), (***) необходимо получить уравнение, содержащее только искомые контурные токи. В соответствии со сказанным с помощью (***) заменяем в основном уравнении (*) напряжения на токи ветвей, которые затем выражаем через контурные токи согласно (**):
,
После группировки имеем:
Первое слагаемое здесь представляет сумму напряжений всех резистивных ветвей контура только от собственного контурного тока в отсутствие токов других контуров (при их разрыве), а остальные слагаемые—напряжения ветвей контура от токов других контуров в отсутствие собственного контурного тока. В правую часть перенесены напряжения всех источников, входящих в контур.
Аналогичные уравнения получим для остальных контуров. Если число контуров равно п, то предположив для общности число ветвей каждой ячейки также равным п, можно записать систему уравнений контурных токов:
Коэффициент Rkk—собственное сопротивление контура, равное сумме сопротивлений всех ветвей ячейки, а коэффициент Rik=Rki (i<>k) – взаимное сопротивление контуров, равное сопротивлению общей для контуров i и k ветви, взятому с отрицательным знаком, которым учитываются встречные направления контурных токов в рассматриваемой ветви.
Каждое уравнение системы выражает условие равновесия напряжений ветвей контура – резистивных и источников напряжения (в правой части). Слагаемое на главной диагонали 
дает напряжение всех резистивных ветвей только от собственного контурного тока, а слагаемое Рkjij=ukj - напряжение на взаимном сопротивлении контуров только от тока в j-м контуре.
Перейти на страницу: 1 2 3 4 5 6 7