Общая гидродинамика
(4)
Эта группа формул показывает, что проекции поверхностной силы, приложенной к любой наклонной площадке, могут быть выражены через девять величин 
. Это свойство напряжений напоминает аналогичное свойство перемещений частиц и других величин, которые являются тензорными величинами.
Легко показать, что совокупность величин образует тензор. Действительно, уравнения (4) можно рассматривать как линейное преобразование вектора 
в физический вектор 
; коэффициенты преобразования образуют при этом физический тензор. Этот тензор 
называется тензором напряжений. Можно написать в принятом ранее смысле:
(5)
Доказанная тензорность напряжений позволит нам в дальнейшем сделать ряд необходимых выводов. Далее также будет доказана симметричность тензора напряжений.
2. Уравнения движения произвольного объёма жидкости, выраженные через напряжения. Симметричность тензора напряжений. Уравнение непрерывности (сохранения массы).
Рассмотрим некоторый конечный объём жидкости t, ограниченный поверхностью s; пусть плотность жидкости равна r, объёмные силы обозначены через 
и отнесены к единице массы. Применим к нашему объёму принцип Даламбера; на основании которого уравнениям движения системы частиц можно придать форму уравнений равновесия, если к приложенным физическим силам присоединить фиктивные силы инерции. Вспомним также принцип отвердевания, формулируемый так: “если некоторой жидкий (вообще деформируемый) объём находится в равновесии, то при затвердевании его равновесие не нарушится”.
Последний принцип даёт возможность утверждать, что в число уравнений равновесия жидкости (равновесия в Даламберовском смысле) во всяком случае входить условия равновесия соответствующего твёрдого тела. То есть, что условия равенства нулю главного вектора и главного момента приложенных сил являются необходимыми (но, конечно не достаточными) условиями равновесия жидкого объёма.
Итак, имеем условие равенства нулю главного вектора:
(6)
и равенство нулю главного момента:
(7)
Рассмотрим сначала уравнение (6). Превратим второй поверхностный интеграл в объёмный, для этого основываясь на формуле (3) перепишем его в виде:
и применим к каждому из входящих сюда интегралов вторую интегральную формулу, тогда получим:
(8)
Подставляя в (6) найдём:
(9)
откуда в силу произвольности выбранного объёма следует:
(10)
Это и есть искомое уравнение движения жидкости, выраженное через напряжения.
Обратимся к рассмотрению уравнения (7). Аналогично только что проделанному преобразованию перепишем поверхностный интеграл в виде:
и затем применим вторую интегральную формулу
тогда будем иметь, подставляя в (7):
(11)
По (10) второй сомножитель некоторого произведения, входящего под знак первого интеграла обращается в нуль, остаётся:
откуда в силу произвольности t следует:
(12)
Возьмём проекцию этого равенства на первую ось 
:
откуда следует:
Аналогичным путём, проектируя (12) на 
и 
, найдём, что вообще:
(13)
Таким образом равенство нулю главного момента приводит к условиям симметричности тензора напряжений.
Обычно в теории упругости (и сопротивления материалов) составляющие напряжений с разными индексами 
при 
называют касательными напряжениями, так как они лежат в плоскости площадки, к которой приложено полное напряжение. Составляющие с одинаковыми индексами 
называют нормальными напряжениями. Полученное равенство (13) представляет ничто иное, как известную в сопротивлении материалов теорему взаимности касательных напряжений.
Итак, из двух некоторых условий равновесия жидкого объёма по принципу Даламбера, получено только одно векторное уравнение движения жидкости (10). Имея в виду дальнейшие его преобразования, перепишем ещё его в проекциях:
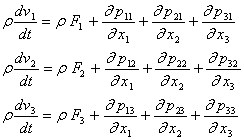(14)
В этой системе, при заданных объёмных силах 
имеем три неизвестных проекции скорости 
, 
, 
и шесть неизвестных проекций напряжений (по условию симметричности тензора напряжений), кроме того мы не знаем ещё как изменяется плотность r жидкости в зависимости от изменения времени, скоростей и др. Таким образом, перед нами стоит совершенно неопределённая задача, что и можно было ожидать, так как мы написали только уравнения для твёрдого объёма, совершенно не принимая во внимание его деформации. Естественно, что мы не сможем обойтись без дополнительных физических предположений. Делая ряд физических гипотез о внутренних силах и деформациях жидкого объёма, мы в дальнейшем доопределим нашу задачу.
Перейти на страницу: 1 2 3 4 5