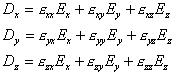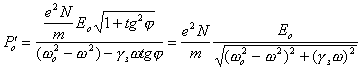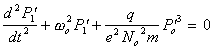Появление мощных источников когерентного светового излучения
Сравнив полученное решение с (3), получаем
|
|
(7a) |
Т.е. восприимчивость является нелинейной функцией напряженности поля. Если же поле достаточно слабое (значительно меньше внутриатомного), то вторым членом можно пренебречь (это означает, что смещение r мало и в выражении для FУ мы пренебрегаем членом qr3) и восприимчивость становится постоянной величиной.
До этого мы рассматривали случай изотропной среды. Когда среда анизотропна, восприимчивость и проницаемость вместо скаляров становятся тензорами второго ранга, а связь между векторами P', D, E имеет вид
|
|
(8) |
dij - единичный тензор.
Для декартовой системы координат:
|
|
(8a) |
Зная параметры внешнего электрического поля и тензор восприимчивости для данного кристалла, обычно определяемый экспериментальными методами, можно всегда рассчитать его поляризацию.
Поляризация диэлектрика в световом поле
Рассмотрим поляризацию диэлектрика в высокочастотном поле на той же простейшей модели газа. Поскольку напряженность электрического поля теперь зависит от времени, необходимо решать динамическую, а не статическую задачу для движения электрона. Уравнение движения электрона запишется в виде
|
|
(9) |
где FT - сила трения пропорциональна скорости движения электрона (так мы учитываем возможные потери энергии электроном); FE - сила, действующая со стороны внешнего электрического поля; FУ - упругая сила. Упругую силу возьмем в линейном приближении (для случая слабого поля): FУ = - k r. Подставив в (9), получим:
|
|
(10) |
Последнее уравнение получено заменой r на выражение через поляризацию из (4), за w02 принято k/m.
Пусть поле меняется по гармоническому закону E(t) = E0 cos wt, тогда решение для поляризации будем искать в виде P' = P'0 cos(wt+j). Дифференцируя это выражение нужное число раз, подставим его в (10):
|
(w02 - w2) P0 (cos wt cos j - sin wt sin j) - - gзwP0 (cos wt sin j + sin wt cos j) = e²N/m E0 cos wt |
(10a) |
Приравняем по отдельности члены при cos wt и sin wt нулю:
|
- (w02 - w2) sin j - gзw cos j = 0 (w02 - w2) P0 cos j - gзwP0 sin j = e2 N E0 / m |
(11) |
Из первого равенства определяем фазу поляризации
|
|
(12) |
и подставив во второе, получим
|
|
(11a) |
Очевидно, решение для поляризации имеет вид
|
|
(13) |
Выводы:
1. Поляризация меняется с той же частотой w, что и внешнее поле.
2. Амплитуда поляризации существенно зависит от соотношения частот w и w0.
a. Если w=w0 (резонанс), амплитуда максимальна;
b. Вдали от резонанса |w-w0| >> gз ![]()
В этом случае фаза поляризации близка к нулю (см. (12)). Тогда поляризация
|
|
(13a) |
т.е. восприимчивость зависит от частоты.
c. В предельном случае постоянного поля для восприимчивости получаем вновь формулу аналогичную (7а) (w=0 ® (13a)): ![]()
До сих пор предполагалось, что на электрон действует поле малой напряженности. Мы брали FУ = - k r (линейное приближение, пригодное для случая малого смещения электрона). Теперь будем считать, что напряженность светового поля и смещение электрона могут быть достаточно большими, и для упругой силы возьмем FУ = - k r - q r3:
|
|
(14) |
|
|
(15) |
Будем, как и раньше считать, что поле E(t) меняется по гармоническому закону, рассматривая нерезонансный случай (|w-w0| >> gз). Членами при gз и P' 3 пренебрегаем. Решение опять ищем в виде P'=P'0+P'1 (два порядка малости), подставляем его в (15) и собирая отдельно члены нулевого и первого порядков малости, получаем:
|
|
(16) |
|
|
(17) |
Перейти на страницу: 1 2 3 4 5 6 7 8