Упругий и неупругий удар двух однородных шаров
Упругий и неупругий удар двух однородных шаров
1. Введение
Столкновения движущихся тел присущи всем уровням Мироздания – от микроскопического до космического, поэтому ударные явления весьма многообразны. В динамике изучают влияние соударений на движение механических систем. Эта задача привлекала внимание многих известных ученых, включая Х. Гюйгенса, И. Ньютона, Ж. Даламбера, С. Пуансона, Г. Дарбу, Э. Дж. Рауса, А.М. Ляпунова, Н.Е. Жуковского, С.П. Тимошенко и многих других. Специфика ударов состоит в их интенсивности и скоротечности. Данное свойство может оказаться и полезным, как при забивке свай, добыче руды или игре в мяч, и опасным, как при транспортных происшествиях. Следовательно, проблема удара важна не только для теоретиков, но и для конструкторов, автолюбителей, спортсменов и др. Биометрия. СКУД и УРВ. Видеонаблюдение https://mosmt-t.ru -☎ +7 (495) 685 93 17
2. Подходы в теории удара
С физической точки зрения ударные силы – отклик на деформации, возникающие вблизи площадки контакта и волнообразно распространяющиеся в данных телах. Математические модели отражают этот процесс с большей или меньшей полнотой. В классической теории удара деформации не учитываются и проблема сводится к определению интегральных характеристик ударных сил – их импульсов. В основе этой теории лежат законы механики и некоторые дополнительные гипотезы.
Рассмотрим для примера простейшую задачу о прямом ударе двух шаров с массами m1 и m2.
|
На рисунке шары массой m1 и m2. до соударения имеют
скорости v1- и v2- требуется найти их скорости после удара.
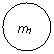 | 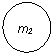 | ||||||
Закон сохранения импульса выражается формулой:
m1 v1i + m2 v2i = m1 v1 + m2 v2
где v1i и v2i ; v1 и v2 соответствуют до – и послеударным значениям скоростей. Этого единственного уравнения недостаточно для определения двух неизвестных v1 и v2. Чтобы построить единственное решение, можно принять одну из следующих гипотез: суммарная кинетическая энергия при ударе сохраняется (абсолютно упругий удар), шары после удара не разделяются, т.е. v1 = v2 (абсолютно неупругий удар). Можно выбрать более общую гипотезу Ньютона, согласно которой
v2 - v1 = e ( v1i - v2i )
Коэффициент восстановления e, как экспериментально установил Ньютон, зависит от материала шаров и лежит в пределах от нуля до единицы.
Волновая теория удара, восходящая к Б. Сен – Венану, наиболее полно описывает напряженное состояние соударяемых тел. В ее основе лежит довольно сложные уравнения математической физики, допускающие точное решение лишь в исключительных случаях. В общем случае использование волновой теории нецелесообразно, в частности, с ее помощью не удается решить рассмотренную задачу об ударе шаров.
Компромиссом между этими двумя крайними подходами служат модели, частично учитывающие деформации. Идею таких методов предложил Даламбер, который мысленно помещал маленькую пружинку (деформируемый элемент) в точку ударного контакта. С математической точки зрения проблема удара сводится к решению обыкновенных дифференциальных уравнений, что не представляет принципиальных трудностей. В вышеприведенном примере идеальная пружинка не рассеивает энергию, поэтому удар будет абсолютно упругим.
3. Упругое соударение тел
При упругом соударении тел тела претерпевают упругую деформацию. При этом кинетическая энергия движущихся тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Взаимодействующие тела представляют собой замкнутую систему, если на них не действуют силы со стороны других тел. В замкнутых системах выполняются законы сохранения энергии и импульса. Зная движение тел до столкновения и применяя законы сохранения, можно определить движение тел после столкновения. Но при этом мы ничего не узнаем о том, как происходит само столкновение. Для решения же ряда задач о столкновении микрочастиц, как правило, достаточно знать об их движении после взаимодействия. "Моделью" для задач подобного рода служит задача о столкновении шаров. Если шары катаются по гладкой горизонтальной поверхности, и если силой трения качения можно пренебречь, то систему из двух шаров можно считать замкнутой. Существует два предельных вида удара: абсолютно неупругий и абсолютно упругий.
Столкновение (соударение) - это кратковременное взаимодействие, при котором тела непосредственно касаются друг друга.
Анализ явлений, имеющий место при ударе упругих сплошных тел, довольно сложен, поэтому рассмотрим самый простой случай - центральное соударение двух однородных шаров. Соударение называется центральным, если векторы скорости шаров до удара направлены по прямой, проходящей через их центры.
Абсолютно упругие и неупругие столкновения - это идеальные случаи. На практике они могут быть реализованы лишь с определенной степенью приближения. В произвольном случае соударения шаров справедливы законы сохранения импульса и энергии:
Абсолютно упругим называется такой удар, после которого во взаимодействующих телах не остается никаких деформаций и суммарная кинетическая энергия, которой обладали тела до удара, равна кинетической энергии тел после удара. Чтобы удар был абсолютно упругим, взаимодействующие тела должны обладать определенными свойствами. А именно, силы, возникающие при ударе, должны зависеть от величины деформации и не зависеть от ее скорости. Наиболее близкими к этим свойствами обладают хорошие сорта стали, слоновая кость. Соударение таких тел происходит следующим образом. При ударе возникают деформации соударяющихся тел, а значит и силы, сообщающие ускорения обоим телам, в противоположных направлениях. В какой то момент времени скорости шаров становятся равными, деформации достигают максимального значения, силы продолжают действовать, изменяя скорости в тех же направлениях, что и раньше. Поэтому шары будут "отодвигаться" друг от друга, а деформации уменьшаться пока совсем не исчезнут. К этому моменту времени упругие силы, возникающие в телах, совершат такую же работу, какая была затрачена на деформацию. В результате вся кинетическая энергия, которой обладали тела до удара, снова перейдет в кинетическую энергию тела после удара. Для определения скорости тел после упругого взаимодействия рассмотрим удар двух шаров (материальных точек), образующих замкнутую систему.
Перейти на страницу: 1 2 3 4 5
