Фильтрация газов - Дипломная работа
1.3. Описание задачи
Рассмотрим температурную задачу в полярной системе координат, где среда представлена одной бесконечной областью (рис.1). Область является пористой и насыщена газом. Будем рассматривать случай радиального движения газа из бесконечности к скважине радиуса 
, ось которой совпадает с осью 
Рис. 1. постановка задачи
При описании температурной задачи примем следующие допущения:
- пористый пласт считается однородным и изотропным по гидродинамическим и теплофизическим свойствам;
- давления в скважине и на контуре питания остаются неизменными;
- породы, окружающие пласт предполагаются непроницаемыми и однородными по своим теплофизическим свойствам;
- температуры газа и скелета пористой среды в каждой точке совпадают;
- естественное тепловое поле Земли считается стационарным;
- пласт расположен на глубине порядка 1 – 2 км, поэтому суточные и сезонные колебания температуры не достигают пласта;
- адиабатическим эффектом, обусловленным гравитационным полем пренебрегаем.
1.4. Математическая постановка задачи
Математическая постановка задачи включает температурную задачу, гидродинамическую задачу, уравнение состояния и соотношение для поля скорости конвективного переноса тепла. Ниже рассматриваются соответствующие постановки задач.
1.4.1. Математическая постановка температурной задачи
Математическая постановка задачи для всех областей представляется уравнением (I.2.1). Температурное поле в этом случае описывается уравнением Чекалюка в пренебрежении теплопроводностью и адиабатическим эффектом и с учетом закона фильтрации Дарси:
|
|
(I.4.1.1) |
. Будем рассматривать задачу при следующих условиях температуры:
начальном
|
| (I.4.1.2) |
, и граничном
|
| (I.4.1.3) |
. 1.4.2. Математическая постановка гидродинамической задачи
Математическая постановка гидродинамической задачи в полярной системе координат примет следующий вид. Учитывая, что для осесимметричного течения поле давления является функцией координаты r уравнение можно представить в виде:
|
|
(1.4.2.1) |
, Будем рассматривать задачу при следующих условиях. Пусть PC – давление на границе контура питания. При значении радиуса, равном радиусу контура питания
|
|
(1.4.2.2) |
, давление поддерживается равным Рс:
|
|
(1.4.2.3) |
, Pс – давление на контуре питания.
При значении радиуса, равном радиусу скважины
|
|
(1.4.1.3) |
, давление поддерживается равным PW:
|
|
(1.4.1.4) |
, где PW – давление в скважине.
1.4. Основные идеи метода характеристик[6]
В данном разделе рассмотрим метод характеристик. Любое линейное дифференциальное уравнение второго порядка (при двух независимых переменных) может быть записано в следующем виде:
|
|
(1.4.1) |
где а, b, с, d, e, f, g — заданные непрерывные функции от x и y (или в частном случае, постоянные).
Попытаемся упростить это уравнение с помощью замены независимых переменных:
|
|
(1.4.2) |
Здесь x и h — новые независимые переменные. Функции j и y, связывающие новые переменные со старыми, будут подобраны позднее; пока же мы будем считать их дифференцируемыми нужное число раз. Кроме того, будем считать, что система уравнений (1.4.2) может быть однозначно разрешена относительно х и у; это надо понимать следующим образом: если функции j и y и отображают некоторую область G плоскости Оху в область G* плоскости Oxh, то при этом каждой точке (x ,h) области G* соответствует только одна точка области G (иначе говоря, отображение области G на G*, даваемое функциями j и y, является взаимно однозначным). Как известно, для этого достаточно, чтобы якобиан преобразования (т. е. определитель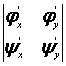 
) нигде в области G не обращался в нуль.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13