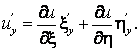Фильтрация газов - Дипломная работа
Для того чтобы сделать требуемую замену переменных, выразим частные производные от функции u по х и у через производные от и по x и h:
|
|
(1.4.31) |
|
|
(1.4.32) |
Это записано на основании правила дифференцирования сложной функции от двух переменных (здесь u зависит от x и h, которые, в свою очередь, зависят от x и у). Для того чтобы выразить 
, через производные по x и h, учтем формулу (1.4.31) и применим снова правило дифференцирования сложной функции:
|
|
Следовательно,
|
|
(1.4.41) |
Аналогично найдем:
|
|
(1.4.42) |
|
|
(1.4.43) |
Правые части равенств (1.4.31), (1.4.32), (1.4.41), (1.4.42), (1.4.43) представляют собой линейные функции относительно частных производных 
, 
Подставляя u'x, u'y, u'xx, . из этих формул в уравнение (1), мы получим снова линейное уравнение второго порядка с неизвестной функцией и и независимыми переменнымиx и h:
|
|
(1.4.5) |
где
|
|
(1.4.5’) |
a 
— функция, линейная относительно и’x , u’h , u .
Уравнение (1.4.5) становится особенно простым, если в нем коэффициенты а и с окажутся равными нулю. Для того чтобы первоначально заданное уравнение (1.4.1) можно было привести к такому простому виду, надо в нем сделать замену переменных
|
|
подобрав функции j и y так, чтобы они являлись решениями уравнения:
|
|
(1.4.6) |
Это уравнение является нелинейным уравнением в частных производных первого порядка. Следующая теорема покажет, как связаны его решения с общим решением некоторого обыкновенного уравнения.
Теорема. Для того чтобы функция z = f(x, у) во всех точках области G удовлетворяла уравнению (6), необходимо и достаточно, чтобы, семейство
|
|
(1.4.7) |
было общим интегралом уравнения
|
|
(1.4.8) |
в той же области G.
Доказательство. Необходимость. Пусть z = f(x, у)— решение уравнения (1.4.6). Рассмотрим семейство кривых f(x, у) — k и докажем, что любая кривая этого семейства удовлетворяет уравнению (1.4.7).
В любой точке, лежащей на кривой f(x, у) = k (где k — фиксировано), выполняется следующее равенство:
|
|
действительно вдоль данной кривой функция f(x, у) постоянна, и поэтому ее полный дифференциал равен нулю.
Следовательно, всюду на кривой имеет место равенство:
|
|
обозначим каждое из этих отношений через l; тогда
|
|
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13