Колебания витка с током
Содержание
Введение
1. Гармонические колебания и их характеристики.
2. Колебания витка с током в магнитном поле
3. Численное решение задачи.
Заключение
Список литературы
Введение Ввгнг ls цена кабель ввгнг.
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процесс широко распространены в природе и технике, например качания маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и другие. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природы. Например ,единый подход к изучению механических и электромагнитных колебаний применялся английским физиком Д. У. Релеем (1842-1919), а А.Г. Столетовым, русским инженером-экспериментатором П.Н. Лебедевым (1866-1912). Большой вклад в развитие теории колебаний внесли: Л.И. Мандельштам (1879-1944) и его ученики.
Целью данной курсовой работы является изучение колебаний магнитного диполя (витка с током). В соответствии с целью автор работы ставит перед собой следующие задачи:
1. Определить положение устойчивого равновесия и рассмотреть колебания магнитного диполя (витка с током) в однородном магнитном поле.
2. Найти собственную частоту колебаний системы, задав её параметры.
3. Построить графики и фазовые траектории.
Основой для выполнения курсовой работы служат учебные пособия по физике и математике Савельева И.В. и Пискунова Н.С.
1. Гармонические колебания и их характеристики.
Колебания называются свободными (или собственными), если они совершаются за счет первоначально совершенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам :
1. Колебания встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;
2. Различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний.
Гармонические колебания величины s описываются уравнением типа
s =A cos (w0 t +j), (1)
где:
n А - максимальное значение колеблющейся величины, называемое амплитудой колебания,
n w0 - круговая (циклическая) частота,
n j - начальная фаза колебания в момент времени t=0,
n (w0 t +j) - фаза колебания в момент времени t.
Фаза колебания определяет значения колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от 1 до -1, то s может принимать значения от +А до -А.
Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение равное 2p, т.е.
w0(t+T)+ j=(w0t+ j)+2p,
откуда
T=2p/w0 (2)
Величина, обратная периоду колебаний,
n=1/T (3)
т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (2) и (3), получим
w0=2p n.
Единица частоты - герц (Гц): 1 Гц - частота периодического процесса, при которой за 1 секунду совершается 1 цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:
(4)
(5)
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (5) и (4) соответственно равны 
и 
.Фаза величины (4) отличается от фазы величины (1) на p/2, а фаза величины (5) отличается от фазы величины (1) на p. Следовательно, в моменты времени, когда s=0, 
приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то 
приобретает наибольшее положительное значение (см. рисунок 1).
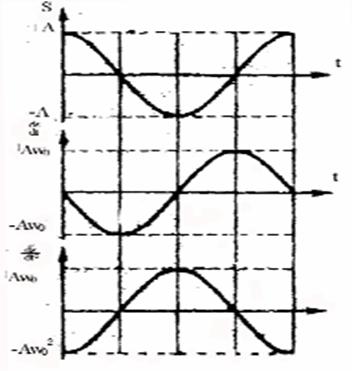
Рисунок 1.
Из выражения (5) следует дифференциальное уравнение гармонических колебаний
, (6)
где s =A cos (w0 t +j). Решением этого уравнения является выражение (1).
Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.
Для этого из произвольной точки О, выбранной на оси x под углом j,равнымначальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде А рассматриваемого колебания (см. рисунок 2).
Рисунок 2.
Если этот вектор привести во вращение с угловой скоростью w0, равной циклической частоте колебаний, то проекция конца вектора будет перемещаться по оси x и принимать значения от -А до +А , а колеблющаяся величина будет изменяться со временем по закону s =A cos (w0 t +j). Таким образом, гармоническое колебание можно представить проекцией на некоторую произвольно выбранную ось вектора амплитуды А, отложенного из произвольной точки оси под углом j, равным начальной фазе, и вращающегося с угловой скоростью w0 вокруг этой точки.