Колебания витка с током
 |
S
0
R ![]()
![]() φ
φ ![]()
![]()
Рисунок 5. Силы, действующие на контур (виток с током).
Магнитный момент, действующий на виток с током:
![]() .
.
Момент инерции витка относительно оси вращения:
![]() .
.
Тогда основное уравнение динамики вращательного движения в данном случае примет вид:
 . (12)
. (12)
Будем рассматривать малые колебания. Тогда: sinφ≈φ. Поэтому из (12):
 ;
;
 . (13)
. (13)
Т.к. ![]() , то
, то ![]() . Тогда из (5):
. Тогда из (5):
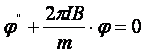 . (14)
. (14)
Характеристическое уравнение для (14):

поэтому общее решение для (14):
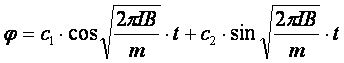 , (15)
, (15)
![]() .
.
Выражение (15) – уравнение гармонических колебаний витка с током в магнитном поле.
Собственная частота колебаний:
 ; (16)
; (16)
 ;
;
период колебаний:
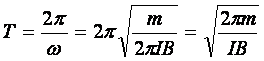 ; (17)
; (17)
 .
.
Выражение (15) можно представить в виде:
![]() . (18)
. (18)
отсюда: ![]() (19)
(19)
Приравниваем (15) и (19):
![]() ; тогда:
; тогда:
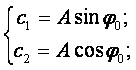
 (20)
(20)
 (21)
(21)
Зададим в (15) начальное условие: ![]()
 .
.
Тогда: ![]() .
.
Уравнение колебаний контура примет вид:
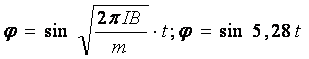 . (22)
. (22)
Построим график функции (22):

Заключение
В данной курсовой работе рассмотрены основные положения теории гармонических колебаний, проведён анализ колебаний витка с током в магнитном поле, получены выражения механического момента, действующего на контур с током, выведено уравнение колебаний контура, найдены период и частота колебаний, построен график колебаний контура.
Список литературы
1. И.В. Савельев. Курс общей физики. Издание пятое. т. 1, глава 9, т.2 глава 13.
2. М.И. Рабинович. Введение в теорию колебаний и волн. М., 1979 г.
3. Н.С. Пискунов. Дифференциальное и интегральное исчисления для втузов., т.2, М., Наука, 1978г.
4. Г. Пейн. Физика колебаний и волн. М., 1969 г.
5. Г.С. Горелик. Колебания и волны. М., 1969 г.
6. Д.В. Сивухин. Общий курс физики. Механика, т.1, электричество, т.3.М., 1977 г.
7. А.А. Покровский. Демонстрационный эксперимент по физике. Том 2. – М. «Просвещение», 1972г.
