Методы расчета электрических полей (конспект лекций)
, 
, 
,
и
.
Введение скалярного потенциала электрического поля позволяет существенно упростить расчет распределения электрического поля. Как известно, дивергенция вектора выражается в общем случае через частные производные всех трех его составляющих. Поэтому, если в пространстве задано распределение r, то найти вектор 
(и в соответствии с соотношением (1.2) вектор 
) непосредственно из уравнения (1.1) можно только в простейших случаях, когда вектор имеет, например, только одну составляющую. В общем же случае решение становится возможным с помощью потенциала, позволяющего исключить из уравнений (1.1) и (1.2) векторы и , и получить связь между потенциалом j плотностью заряда r.
Исключить вектор из уравнения (1.1) можно за счет постановки выражения (1.7) в соотношение (1.2):
.
Подставляя полученное соотношение в уравнение (1.1) получаем
.
Как было сказано выше, мы ограничиваемся рассмотрением задач, в которых среда является кусочно-однородной, т.е. состоящей из участков, с постоянной диэлектрической проницаемостью в пределах данного участка. Для каждого такого однородного участка можно вынести 
за знак дивергенции. Тогда
,
или
, (1.8)
где 
. Уравнение (1.8) называется уравнением Пуассона.
В подавляющем большинстве случаев электрические поля создаются заряженными проводниками. В этом случае все заряды являются поверхностными, т.е. они распределены по поверхностям проводников, являющимися границами электрического поля. Поле существует только в диэлектрике, а внутри проводников напряженность поля равна нулю (иначе в проводнике был бы ток). В этом случае плотность объемного заряда r равна нулю и после описывается уравнением Лапласа
. (1.9)
Как было отмечено выше, тангенциальная составляющая напряженности электрического поля на поверхности проводника равна нулю (1.5). Это означает, что силовые линии перпендикулярны поверхности проводника и потенциал вдоль поверхности не изменяется. Но потенциал не может меняться и вглубь проводника. Поэтому в электростатическом поле для поверхности проводника справедливо граничное условие
, (1.10)
позволяющее говорить о постоянстве потенциала всего проводника.
Таким образом, электростатическое поле в любой области пространства, в которой диэлектрическая проницаемость среды e постоянна, описывается уравнением Пуассона (1.8) относительно скалярного потенциала j или эквивалентными ему уравнениями (1.1) и (1.2) относительно вектора напряженности поля . Связь между j и устанавливается соотношением (1.7). На границах раздела между областями пространства с различными значениями e выполняются граничные условия (1.3) и (1.4). На поверхностях проводников выполняется условие (1.5), из которого вытекает условие эквипотенциальности поверхности проводника (1.10).
2. Расчет простейших электростатических полей методом изображений
3. Интегральные методы расчета электростатических полей
3.1. Общая характеристика интегральных методов
Интегральные методы расчета электростатических полей развивают идею, заложенную в методе изображений, в котором поля реальных проводящих тел моделируются полями систем простейших зарядов (точечных или линейных), а значения последних находятся из условия эквипотенциальности поверхности проводников.
Идея интегральных методов заключается в следующем. Реальные распределения заряда по поверхностям тел полеобразующей системы замещаются фиктивными распределениями по некоторым поверхностям, лежащим внутри реальных тел. Эти фиктивные распределения заряда определяются из условия эквипотенциальности поверхности проводников (1.10), а также из условий неразрывности тангенциальной составляющей вектора напряженности электрического поля (1.3) и нормальной составляющей вектора электрического смещения (1.4) на границах раздела диэлектриков.
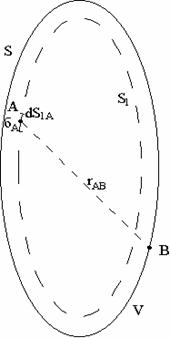
Рассмотрим суть интегральных методов на примере расчета электростатического поля проводящего тела, помещенного в однородную среду с диэлектрической проницаемостью e, которое ограничено поверхностью 
, и к которому приложено напряжение V (рис. 3.1).
|
Рис. 3.1. К расчету электростатического поля интегральным методом. |
Пусть внутри тела по поверхности 
распределен заряд с неизвестной плотностью s. Рассчитаем потенциал, наведенный этим распределенным зарядом в произвольной точке B поверхности . Для этого на поверхности возьмем произвольную точку A и выделим в ее окрестности бесконечно малую площадку 
, плотность заряда на которой обозначим 
. Тогда потенциал в точке B определяется как
Перейти на страницу: 1 2 3 4 5