Алескандрия как центр античной науки
Знаменитые Александрийцы.
a. Герон Александрийский
Герон Александрийский; Heron, Ι в. н.э., греческий механик, инженер и математик. Время его жизни неопределенно, известно только, что он цитировал Архимеда ( который умер в 212 г до н.э. ), его же самого цитировал Папп (ок. 300 г н.э.). в настоящее время преобладает мнение, что он жил в Ι в. н.э Занимался геометрией, механикой, гидростатикой, оптикой; изобрел прототип паровой машины и точные нивелировочные инструменты. Математические работы Герона являются энциклопедией античной прикладной математики. Работы его дошли до нас не полностью. Из его работ известны "Механика", "Книга о подъемных механизмах", "Пневматика", "Книга о военных машинах", "Театр автоматов", "Метрика", " О диоптре", "Катоптрика".
В "Метрика" приводятся правила и указания для точного и приближенного вычисления площадей (правильных многоугольников) и объемов различных фигур ( усеченных конусов, пирамид и т.д.) и тел; среди них имеется и формула для определения площади треугольника по трем его сторонам, вошедшая в математику под именем формулы Герона.
Вывод формулы Герона имеет следующий вид: Известно, как находить площадь треугольника, если известны две его стороны и угол между ними. А что делать, если даны три стороны a, b и c? Надо найти угол между сторонами a иb, благо мы это уже умеем. Точнее, нам нужен не сам угол, а его синус. Его мы найдем так: из теоремы косинусов запишем 
и воспользуемся формулой 
(для произвольных
, как вы помните, в правой части может стоять минус, но если - угол в пределах от 
до
, то 
, так что в этом случае минус не нужен). Подставляя все это в нашу формулу для площади треугольника, получим вот что
( 
- площадь треугольника ):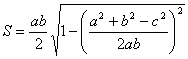 
Это выражение можно преобразовать к более приятному виду. Для этого обозначим буквой 
величину 
, ( - половина периметра треугольника, коротко - полупериметр). Тогда после упрощений получим: Площадь треугольника со сторонами, a, b и c равна 
, где 
.
Эта формула называется формулой Герона.
Кроме того, в этой работе указываются примеры решения квадратных уравнений и кубических корней. Характерной особенностью «Метрики», выделяющей ее из ряда работ других греческих геометров, предшествовавших Герону, служит то обстоятельство, что в ней обычно правила даются без доказательств, а лишь выясняются на отдельных примерах. Это значительно снижает достоинства работы и, несомненно, является признаком недостаточной научной подготовки её автора. Лучшей иллюстрацией этого является его работа «О диоптре». В этом труде изложены правила различных работ геодезического характера, причем землемерная съемка производится с помощью изобретенного Героном прибора диоптры. Там же дается описание диоптра – прибора для измерения углов – прототипа современного теодолита. Главной его частью служила линейка с укрепленными на концах ёе визирами. Эта линейка вращалась по кругу, который мог занимать и горизонтальное, и вертикальное положение, что давало возможность намечать направления как в горизонтальной, так и в вертикальной плоскости. Для правильности установки прибора к нему присоединялись отвес и уровень. Пользуясь этим прибором и вводя фактически в употребление прямоугольные координаты, Герон мог решать на местности различные задачи. А именно измерить расстояние между двумя точками, когда одна из них или две недоступны наблюдателю; провести прямую, перпендикулярную к недоступной прямой линии; найти разность уровней между двумя пунктами; измерить площадь простейшей фигуры, не вступая на измеряемую площадку.
В трактате "Катоптрика" (катоптрика-наука об отражении лучей от зеркальных поверхностей) Герон обосновывает прямолинейность световых лучей бесконечно большой скоростью их распространения. Далее, он приводит доказательство закона отражения, основанное на предположении, что путь, проходимый светом, должен быть наименьшим из всех возможных. Почти за 1500 лет до Ферма чисто геометрическим путем приходит к частной формулировке его принципа для отражения: "Скажу, что из лучей, падающих из данной точки и отражающихся в данную точку, минимальны те, которые от плоских и сферических зеркал отражаются под равными углами".
Вслед за законом отражения Герон рассматривает различные типы зеркал, особое внимание уделяя цилиндрическим зеркалам. Следуя его трудам, все ученые стали разделять оптику на катоптрику, т.е. науку об отражении и диоптрику, т.е. науку об изменении направления световых лучей при попадании в прозрачные среды, или, как мы теперь говорим, о преломлении.
В произведении этого ученого и инженера, которое называется "Театр автоматов", описано даже устройство целого театра, представление в котором разыгрывали фигурки-куклы, приводимые в движение с помощью системы зубчатых колес, блоков и рычагов. Также для приведения в действие автоматов-игрушек использовали энергию падающего груза, вытекающей из отверстия струи воды или высыпающегося песка. "Театр автоматов" исполнял пьесу, которая передавала легенду о Навплии, относящуюся к временам Троянской войны, - месть Навплия грекам, побившим его сына Паламеда камнями. Пьеса содержала пять актов и восемь картин. В первом акте зритель видел, как данайцы строят корабли перед походом: они пилят, строгают, бьют молотками; слышны соответствующие звуки. Во втором акте люди тянули построенные суда с помощью веревок в воду. В третьем акте перед зрителями открывалась картина спокойного моря с кильватерной колонной парусников и резвящимися в воде дельфинами. Следующая сцена изображала шторм, строй кораблей нарушался, они собирались вместе. В четвертом акте показывалась месть Навплия, который зажигал факел, стоя на скале; при этом присутствовала Афина. Мореплаватели, приняв огонь факела за свет маяка, направляли корабли на скалы. В последнем, пятом акте развертывалась картина кораблекрушения. В волнах появлялся плывущий Аякс, слышался удар грома, и сверкала молния, которой Афина поражала Аякса. Фигура Аякса скрывался в волнах, фигура Афины исчезала, и представление заканчивалось.
Перейти на страницу: 1 2 3 4 5 6 7 8 9