Волны в упругой среде
Рассмотрев кратко основные понятия, связанные с волной, перейдем к описательной стороне, т.е. волновому уравнению.
Волновое уравнение.
Математические сведения.
Этот параграф является математическим введением к тому динамическому рассмотрению волн, которое будет дано в $2. Рассмотрим произвольную функцию
f(at-bx) (2.3) от аргумента аt—bх. Продифференцируем ее дважды по t:
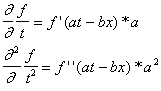(2.4)
Здесь штрих означает дифференцирование по аргументу at—bx. Продифференцируем теперь нашу функцию дважды по х:
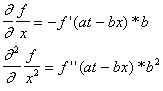(2.5)
Сравнивая (2.4) и (2.5), мы убеждаемся, что функция (2.3) удовлетворяет уравнению
(2.6)
где
u=a/b.
Легко видеть, что этому же уравнению удовлетворяет произвольная функция
f(at+bx) (2.7) (2.7) аргумента at+bx, а также сумма функций вида (2.3) и (2.7).
Функции (2.3) и (2.7) изображают при положительных a, b плоские волны, распространяющиеся, не деформируясь, со скоростью и в сторону соответственно возрастающих или убывающих значений х **).
Уравнение (2.6)—дифференциальное уравнение в частных производных, играющее в физике очень важную роль. Оно называется волновым уравнением. В математических курсах доказывается, что оно не имеет решений, отличных от тех, которые могут быть представлены функциями вида (2.3) и (2.7) или суперпозицией таких функций, например,
f1(at - bх) + f2(at+bx).
Всякий раз, когда из физических соображений можно установить, что та или иная физическая величина s удовлетворяет уравнению вида
(2.6а)
мы сможем на основании сообщенных здесь математических сведений заключить, что процесс изменений этой величины носит характер плоской, волны, распространяющейся в ту или другую сторону со скоростью и, или суперпозиции таких волн.
Вид функций f1, f2 определяется характером движения источника волн, а также явлениями, происходящими на границе среды.
Пусть источником волн является плоскость х=0, причем на этой плоскости величина S колеблется но закону s =Acoswt. В этом случае от плоскости х=0 распространяются вправо и влево волны
s= Acos(wt
kx), k =
.
Из линейности волнового уравнения следует, что если ему удовлетворяют функции s1, s2,s3, . в отдельности, то ему удовлетворяет также функция
S == S1 + S2 + S3 + .
(принцип, суперпозиции).
Рассмотрим несколько примеров.
а) Волновому уравнению удовлетворяют синусоидальные бегущие волны
s1 = Aсоs(wt — kx),s2= Acos(wt+kx).
На основании принципа суперпозиции волновому уравнению удовлетворяет стоячая волна
s=2Acoskx coswt
являющаяся суперпозицией только что рассмотренных синусоидальных бегущих волн.
б) Волновому уравнению на основании принципа суперпозиции удовлетворяет всякая функция вида
S=
Это—функция вида f(at—bx); она изображает несинусоидальную волну, распространяющуюся без деформации в сторону возрастающих х.
|
|
в) Пусть волны S1, S2, имеющие вид коротких импульсов, распространяются навстречу одна другой. В некоторый момент моментальный снимок суперпозиции S1 + S2 этих волн имеет вид, показанный на рис. 4,а. Через некоторое время моментальный снимок волны будет иметь вид, показанный на рис. 4, б, – волны пройдут «одна сквозь другую» и притом каждая так, как будто другой не существует.
Упругие волны в стержне.
волновое уравнение.
В предыдущем параграфе мы рассмотрели математическую сторону волнового уравнения. В этом же параграфе я хотел бы на конкретном примере рассмотреть как работает тот математический аппарат.
|
Рисунок 4 |
Применим второй закон Ньютона и закон сложения сил к движению куска стержня, заключенного между двумя плоскостями x и х+
х. Масса этого куска равна р0S0х, где р0 и S0 – соответственно плотность и сечение в отсутствие деформации. Пусть 
– смещение центра тяжести рассматриваемого куска. Тогда
слева стоит произведение массы куска на ускорение д2/дt2 его центра тяжести, справа – результирующая внешних сил, действующая на кусок.
Разделим уравнение на S0
:
(2.7)
Перейдя к пределу при 
, получим уравнение
(2.8)
справедливое в каждой точке стержня. Оно указывает, что ускорение данной точки пропорционально частной производной напряжения по ж в этой точке.
Подставляя в (2.8) соотношение (2.7), получим:
(2.9)
Вспомнив теперь формулу , содержащую определение деформации, и подставив ее в (2.9), получаем:
(2.10)
Это—волновое уравнение.Оно указывает, что смещение распространяется но стержню в виде волн
(2.11)