Теория поля
Векторное поле изображается при помощи векторных или силовых линий. Векторные линии имеют следующий физический смысл. В каждой точке линии вектор, характеризующий поле, направлен по касательной. О численной величине вектора в точке пространства судят по густоте силовых линий, проходящих через перпендикулярную к ним единицу площади. Продвигаем саи ты по Ремонту строительного инструмента.
Изучение скалярного и векторного полей ведется при помощи использования специальных понятий и формул.
- Что такое градиент скалярного поля?
- Вектор, проекции которого на оси прямоугольных координат являются частными производными от скалярной функции по координатам точки, является градиентом скалярной функции в точке и обозначается 
Проекции градиента на оси координат определяются формулой:
.
Модуль gradU вычисляется по формуле:
.
Для случая плоского поля U(x,y) градиент
есть вектор, лежащий в плоскости x, y и перпендикулярный к линии уровня поля в каждой точке.
Основные свойства градиента:
Итак, скалярное поле характеризуется вектором, который является градиентом функции U(x, y, z). Такие векторы называются п о т е н- ц и а л ь н ы м и, а скалярная функция U(x, y, z) – потенциалом.
Потенциальное поле характеризуется векторными линиями, которые ортогональны к поверхности уровня в каждой точке пространства. В направлении этих линий происходят максимальные изменения функции U(x, y, z).
- Как определяется скорость изменения скалярного поля по заданному направлению?
- Определить скорость можно по формуле, представив в виде скалярного произведения:
Скорость изменения скалярного поля по заданному направлению равна скалярному произведению градиента этого поля на единичный вектор направления.
- Как определятся поток векторного поля?
- Поток вектора 
через поверхность S можно записать в следующем виде:
где An – проекция вектора А на нормаль к поверхности S. Поток есть величина скалярная и зависящая от ориентации поверхности S. При изменении направления нормали, знак проекции, а следовательно, и потока изменится на противоположный.
- Как определятся дивергенция вектора?
- Допустим, что векторные линии поля в рассматриваемом пространстве возникают по всюду. Возьмем в поле точку P0 проведем вокруг нее замкнутую поверхность S, ограничивающую объем 
, вычислим через нее поток вектора и разделим результат на объем. В итоге найдем поток вектора на единицу объема. В пределе при стягивании S в точку частное будет характеризовать интенсивность (или плотность источника) истечения векторных линий из точки P0, т.е. из бесконечно малого объема. Этот предел называется дивергенцией вектора 
в точке 
и обозначается 
Выразим дивергенцию в точке P0 через проекции вектора в этой же точке. Поместим 
внутрь элементарного параллелепипеда с гранями, параллельными координатным плоскостям. Поскольку предел не зависит от форм поверхности S , то выбор такого вида объема не ограничивает общности вывода.
Найдем поток вектора через грани параллелепипеда, затем разделим его на и перейдем к пределу.
Поток вектора через две параллельные грани, перпендикулярные оси Z, равен:
Для граней, перпендикулярных осям x и y, аналогично получим:
В этих выражениях значения производных берутся в точках, расположенных внутри параллелепипеда. Взяв суммарный поток, подставив его в формулу предела, получим:
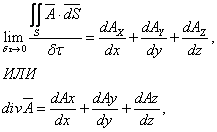
где Аx, Ay, Az – проекции вектора в точке Р0. Производные также берутся по координатам точки Р0.
Дивергенция вектора в точке Р есть величина скалярная и характеризует интенсивность истечения векторных линий из области точки Р0.
Рассмотрим дивергенции суммы векторов и произведения скаляра на вектор. Допустим, что имеем поля векторов А и В и скалярное поле U. Тогда:
- Каков основной смысл формулы Остроградского-Гаусса?
- В 1828 г. известный русский математик Остроградский установил связь между потоком вектора и дивергенцией. Теорема, называемая также теоремой Остроградского-Гаусса, гласит: поток вектора через замкнутую поверхность 
равен интегралу от дивергенции, взятому по объему 
, ограниченному данной поверхностью.
Перейти на страницу: 1 2 3 4 5 6 7 8