Теория поля
В координатной форме формула Стокса имеет вид
- В чем состоит существенное различие операторов Гамильтона и Лапласа? https://www.компания-кондор.рф купить Присадка Сигбол.
- Основные характеристики полей -градиент скалярного поля, дивергенция и ротор векторного поля - определяются при помощи дифференцирования скалярных функций или проекций векторов.
Для более компактной записи этих характеристик английский математик Гамильтон (1805-1865) ввел символический, т.е. не имеющий физического смысла, вектор (набла), называемый также оператором Гамильтона
1.3. Векторные операции в ортогональных криволинейных координатах. Общая характеристика ортогональных криволинейных координат. Выражение элементов длины, площади и объема в криволинейных координатах через прямоугольные. Градиент, дивергенция, ротор в криволинейных координатах. Основные характеристики полей в цилиндрических и сферических координатах.
- Напишите выражение элементов длины, площади и объема в криволинейных координатах через координаты Ламе.
- Выразим элементы длин координатных линий, площади и объема в криволинейных координатах, используя прямоугольные.
|
|
Возьмем координатную линию, расположенную в прямоугольной системе координат. Радиус-вектор точки, расположенной на линии, имеет обычный вид 
где 
; 
; 
. Обозначим элемент дуги координатной линии 
через 
. Поскольку 
, нахождение сведем к нахождению 
.
Известно, что
где 
Отсюда находим
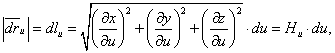
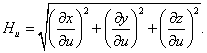
Аналогично
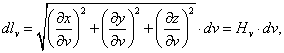
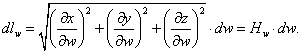
Коэффициенты 
, 
, 
называют коэффициентами Ламе или масштабными множителями криволинейной системы координат.
Зная значения элементов длин координатных линий, запишем выражения для элементов площадей
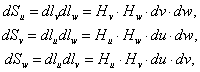
и элемента объема
- Напишите общие выражения градиента, дивергенции, ротора, лапласиана в криволинейных координатах.
- Выражение градиента скалярной функции в криволинейных координатах
Как видим, градиент в криволинейных координатах зависит не только от значения функции 
в точке, но и от значения масштабных коэффициентов данной системы координат и направления единичных орт осей.
Принцип определения дивергенции вектора через его проекции, примененный в случае прямоугольных координат, сохраним и теперь, т.е.
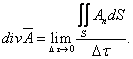
Выражение лапласиана в криволинейных координатах:
Ротор будем искать обычным образом:
Теперь запишем выражение вектора 
:
Выражение удобно записать через определитель
- Чему равны коэффициенты Ламе в цилиндрических и сферических координатах?
- Определим значения коэффициентов Ламе цилиндрических координат. Для этого запишем выражения для элементов длин координатных линий
С другой стороны, известно, что
Сопоставляя попарно эти равенства, приходим к выводу, что
- Связь сферических координат с прямоугольными определяется соотношениями
Элементы длин координатных линий найдем, сопоставляя попарно выражения из двух систем
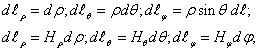
Из этого имеем:
- Запишите выражения градиента, дивергенции, ротора, лапласиана в цилиндрических и сферических координатах.
Перейти на страницу: 1 2 3 4 5 6 7 8