Теория поля
Формулу Остроградского можно записать в форме:
или
Формула широко применяется для преобразования интеграла, взятого по объему, ограниченному поверхностью, в интеграл, взятый по этой поверхности. С помощью формулы бывает удобно также определять поток вектора, не проводя прямых вычислений.
- Какие поля называют соленоидальными и каковы их свойства?
-Соленоидальным называют векторное поле, не имеющее источников. Необходимым и достаточным условием для этого является
Соленоидальные поля обладают рядом общих свойств.
1. Поскольку в соленоидальном поле нет источников, то векторные линии в таком поле не обрываются и не начинаются. Они могут быть только замкнутыми или уходящими в бесконечность.
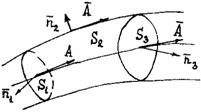2. Поток вектора через любое поперечное сечение векторной трубки есть величина постоянная. Векторной трубкой называют часть пространства, состоящую из векторных линий. Для доказательства этого свойства возьмем в векторной трубке поля 
два сечения и вычислим поток вектора через замкнутую поверхность
- Как определяется циркуляция вектора и какой физический смысл она имеет?
- Возьмем в поле вектора некоторую кривую 
, и найдем работу по перемещению материальной точки вдоль этой кривой из 
т.
в т.
(рис. 2.10). Ре можно определить в виде скалярного произведения 
Работа вектора вдоль всей кривой будет равна 
Уменьшая длину 
и переходя к пределу, получим криволинейный интеграл
Скалярному произведению можно придать другой вид:
где 
- проекция вектора на касательную к кривой .
Криволинейные интегралы записанные выше называют также линейным интегралом вектора вдоль кривой. Если кривая замкнутая, то криволинейный интеграл будет называться циркуляцией. Таким образом, циркуляция имеет смысл работы векторного поля по перемещению точки вдоль замкнутой кривой, т.е.
При вычислении работы обход по контуру совершается против часовой стрелки (в правой системе координат).
- Запишите выражение ротора через проекции вектора.
- Ротор вектора удобно записать через определитель
После раскрытия определителя получаем формулу
Поясним физический и аналитический смысл ротора. Для этого рассмотрим плоское векторное поле 
- линейной скорости частиц сплошной среды, перпендикулярное оси 
. В этом случае проекция скорости на ось и производные по этой оси равны нулю, поэтому
т.е. ротор в каждой точке поля направлен перпендикулярно плоскости заданного поля.
- Дайте определение потенциального поля и перечислите его основные свойства.
- Векторное поле называется потенциальным, если вектор , характеризующий поле, является градиентом скалярной функции 
:
Скалярная функция называется потенциальной функцией или потенциалом вектора .
Если - потенциальная функция, то 
также будет потенциальной.
Потенциальное поле обладает следующими свойствами:
1. Потенциальное поле можно задать не только проекциями вектора, но и одной скалярной функцией - потенциалом.
2. Работа потенциального вектора вдоль некоторой кривой не зависит от формы этой кривой. Она зависит только от положения начальной и конечной точек и равна разности значений потенциала в этих точках.
- Приведите примеры потенциальных полей.
Примерами потенциальных полей являются поле силы притяжения, электростатическое поле, электрическое поле постоянного тока и пр.
- Запишите формулу Стокса.
- Физический смысл формулы Стокса состоит в том, что циркуляция векторного поля по замкнутому контуру равна потоку ротора поля через любую поверхность, ограниченную этим контуром:
Перейти на страницу: 1 2 3 4 5 6 7 8