Рефераты по Физике

Упругие волны

Страница 3

υ.

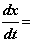
откуда

(2.4)

Таким образом, скорость распространения волны υ в уравнении (2.2) есть скорость перемещения фазы, в связи с чем ее называют фазовой скоростью.

(2.5)

Согласно (2.4) dx/dt > 0. Следовательно, уравнение (2.2) описывает волну, распространяющуюся в сторону возрастания х. Волна, распространяющаяся в противоположном направлении, описывается уравнением

x = a cos [ w ( t + x/υ ) +a ]

– υ,

Действительно, приравняв константе фазу волны (2.5) и продиф­ференцировав получившееся равенство, придем к соотношению

из которого следует, что волна (2.5) распространяется в сторону убывания х.

(2.6)

,

λ

2π

Подпись: k =
Уравнению плоской волны можно придать симметричный отно­сительно х и t вид. Для этого введем величину

Подпись: k =

ω

υ

(2.7)

которая называется волновым числом. Умножив числи­тель и знаменатель выражения (2.6) на частоту v, можно пред­ставить волновое число в виде

(2.8)

(см. формулу (1.2)). Раскрыв в (2.2) круглые скобки и приняв во внимание (2.7), придем к следующему уравнению плоской вол­ны, распространяющейся вдоль оси х:

x = a cos ( wt + kx +a )

Уравнение волны, распространяющейся в сторону убывания х, отличается от (2.8) только знаком при члене kx.

При выводе формулы (2.8) мы предполагали, что амплитуда колебаний не зависит от х. Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При рас­пространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается – наблюдается затухание волны. Опыт показывает, что в однородной среде такое затухание происходит по экспоненциальному закону: a = a0 e–γx. Соответственно урав­нение плоской волны имеет следующий вид:

(2.9)

x = a0 e–γx cos ( wt + kx +a )

(a0 – амплитуда в точках плоскости х = 0).

Теперь найдем уравнение сферической волны. Всякий реаль­ный источник волн обладает некоторой протяженностью. Однако если ограничиться рассмотрением волны на расстояниях от источ­ника, значительно превышающих его размеры, то источник можно считать точечным. В изотропной и однородной среде волна, по­рождаемая точечным источником, будет сферической. Допустим, что фаза колебаний источника равна wt + a. Тогда точки, лежа­щие на волновой поверхности радиуса r, будут колебаться с фазой

Перейти на страницу:  1  2  3  4  5  6  7  8  9  10