Упругие волны
Страница 5
x (x, y, z, t ) = a cos ( wt − kxx – kyy – kzz + a )


Здесь

Функция (3.6) дает отклонение точки с координатами х, у, z в момент времени t. В случае, когда
n совпадает с
ex, kx = k, ky = kz = 0 (и уравнение (3.6) переходит в (2.8). Очень удобна запись уравнения плоской волны в виде
x = Re aei (ωt-kr+α)
Знак Re обычно опускают, подразумевая, что берется только вещественная часть соответствующего выражения. Кроме того, вводят комплексное число
â = aeiα,
которое называют комплексной амплитудой. Модуль этого числа дает амплитуду, а аргумент – начальную фазу волны Таким образом, уравнение плоской незатухающей волны можно представить в виде
x = âei (ωt-kr)
Преимущества такой записи выяснятся в дальнейшем.
§ 4. Волновое уравнение
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции (3.6), описывающей плоскую волну. Продифференцировав эту функцию дважды по каждой из переменных, получим
Сложение производных по координатам дает




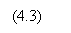


Перейти на страницу: 1 2 3 4 5 6 7 8 9 10

![]()
![]()
![]()
![]()
![]()
![]()
![]()

