Физика твердого тела
Введение примеси в полупроводниковое вещество понижает его сопротивление.
Если в веществе содержится примесь двух типов – и акцепторы, и доноры, то происходит взаимная компенсация примеси. При равенстве концентраций доноров и акцепторов легированный полупроводник подобен собственному. Такие полупроводники называются скомпенсированными. Удаление зуба планерная профессиональная стоматология в москве планерная.
Металлы, диэлектрики и полупроводники в зонной теории.
Полнее всего различия между металлами, диэлектриками и полупроводниками объясняет зонная теория твердого тела.
Энергетические уровни электронов в изолированном атоме расщепляются в энергетическую зону при образовании из этих атомов кристаллической решетки. Если энергетический уровень полностью заполнен, то и образующаяся энергетическая зона будет заполнена целиком. Поскольку по принципу Паули на каждом энергетическом уровне может находиться не более двух электронов, каждая неперекрывающаяся зона содержит 2N состояний и в ней не может быть более 2N электронов. Если имеется f-кратное вырождение уровней, то образующаяся зона будет f-кратно вырождена и может содержать не более 2N f электронов.
Следовательно, если зона целиком заполнена, то переход электронов под действием энергии тепловых колебаний атомов или внешнего поля из одного состояния в другое невозможен, так как по принципу Паули все состояния заняты. В связи с тем, что над полностью занятой разрешенной зоной имеется запрещенная зона, для переброса электрона через которую в следующую разрешенную зону требуется конечная энергия, такой кристалл не будет проводить электрический ток. Такой кристалл будет диэлектриком.
Если ширина запрещенной зоны невелика по сравнению со средней энергией теплового движения, то возможны перебросы электронов из полностью заполненной зоны в следующую разрешенную свободную зону. При этом возникает электропроводность как по не полностью заполненной зоне, так и по следующей частично заполненной зоне. Такой кристалл — полупроводник.
Рис.2.
Если разрешенная зона заполнена не полностью, то электроны могут ускоряться и переходить под действием электрического поля на свободные уровни в пределах одной зоны. Такой материал — типичный металл. Металлическая проводимость образуется и при перекрытии заполненной энергетической зоны с незаполненной зоной.
Расчет эффективных масс плотности состояний для электронов и дырок.
Зона проводимости кремния представляет собой наложение трех ветвей E(k), одна из которых лежит значительно ниже других. Положение абсолютного минимума определяет дно зоны проводимости (Рис.3). Он лежит в направлении [100], поэтому всего имеется 6 эквивалентных минимумов энергии или 6 долин.
Рис.3.Зонная структура кремния.
Изоэнергетические поверхности около абсолютных минимумов представляют собой эллипсоиды вращения относительно большой полуоси, которая совпадает с направлением [100] (Рис.4)
Рис.4. Поверхности равной энергии в зоне проводимости кремния.
Зависимость энергии от к можно представить в виде
.
Опыты по циклотронному резонансу дают для компонентов тензора эффективной массы электрона в кремнии следующие значения: m1=m2=0,19m0; m3=0,98m0.
В соответствии с тем, что имеется 6 эллипсоидов равной энергии, плотность состояний, которая выражается для одного эллипсоида равенством
,
увеличится в 6 раз. Если учесть, что для кремния m1=m2, то
,
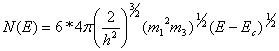а эффективная масса плотности состояний для электронов с учетом значений m1=0,19m0 и m3=0,98m0 будет:
. (1)
Следовательно, у кремния все 6 эллипсоидов изоэнергетической поверхности зоны проводимости можно заменить одной сферической поверхностью с эффективной массой плотности состояний для электронов, равной 1,08m0.
Для валентной зоны максимум энергии находится в центре зоны Бриллюэна к=0 для всех трех полос, при этом в этой точке все три зоны смыкаются, так что энергия в центре зоны Бриллюэна оказывается вырожденной(Рис.5).
Рис.5. Поверхности равной энергии в валентной зоне кремния.
Учет спин-орбитального взаимодействия (тонкой структуры уровней) приводит к тому, что вырождение частично снимается. Связь между энергией и волновым вектором задается формулой:
,
,
где 
и 
- энергии, которые соответствуют тяжелым и легким дыркам соответственно, а 
- отщепленным дыркам, скалярные эффективные массы которых можно посчитать по формулам:
, 
.
- безразмерные константы.
Опыт дает mT*=0,49m0, mЛ*=0,16m0.
Плотность состояний будет определяться суммой плотности состояний в зонах тяжелых и легких дырок:
.
Изоэнергетические поверхности обеих зон можно заменить одной приведенной сферой с плотностью состояний
Перейти на страницу: 1 2 3 4 5