Физика твердого тела
Концентрация акцепторов, при которой наступает полное вырождение:
.
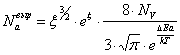Расчет времени жизни носителей заряда.
Реальные полупроводниковые материалы содержат обычно примеси нескольких типов, каждая из которых может создавать один или несколько уровней в запрещенной зоне полупроводника. Дефекты решетки, обычно нейтральные в состоянии термодинамического равновесия и способные захватывать подвижные носители заряда одного знака и освобождать их, называются ловушками захвата. Ограничимся рассмотрением случая, когда в полупроводнике имеется один тип ловушек, создающий энергетический уровень.
Время жизни носителей заряда определяется формулой
.
В случае малого уровня возбуждения, когда 
, время жизни неравновесных носителей заряда имеет вид:
,
,
,
где Sp и Sn – сечения захвата электронов и дырок,
Nt – концентрация рекомбинационных центров,
VT – тепловая скорость.
Расчет s(T). Формулы для подвижности.
Удельная электропроводность примесных полупроводников определяется по формуле s=qnmn для донорного и по формуле s=qpmp для акцепторнрго полупроводника. Для вычисления s(T) необходимо найти температурную зависимость подвижности.
Кремний является неполярным полупроводником. Для него существуют два основных механизма рассеяния, которые существенно влияют на подвижность, а именно рассеяние на акустических фононах и на ионизированных примесях.
При низких температурах, когда число фононов в кристалле сильно уменьшено охлаждением, подвижность определяется рассеянием на ионизованных примесных центрах.
Каждый ионизованный центр в кристалле представляет собой неподвижный отрицательный или положительный заряд, который может отклонить траекторию пролетающего электрона.
Подвижность, связанная с рассеянием на ионах примеси, описывается формулой Бруккса-Херринга:
,
где NI – концентрация ионов примеси, n – концентрация электронов проводимости.
При высоких температурах в Si электроны рассеиваются преимущественно продольными акустическими фононами.
При возникновении продольных акустических колебаний происходит смещение центра тяжести элементарной ячейки и происходит упругая деформация кристаллической решетки, которая приводит к изменению положения краев зоны проводимости и валентной зоны, что адекватно возникновению на пути движения носителей заряда потонциального барьера и рассеянию на нем носителей заряда.
Подвижность, связанная с рассеянием на акустических фононах описывается формулой Бардина-Шокли:
,
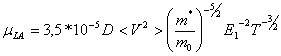где D-плотность; V-скорость звука; E1 – акустический потенциал деформации.
После подстановки коэффициентов получаем для кремния:
, см2/В*с.
Результирующая подвижность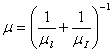 
.
Расчет зависимости RH(T).
Рассмотрим образец для Холловских измерений (Рис.6).
Рис.6. Схема Холловских измерений.
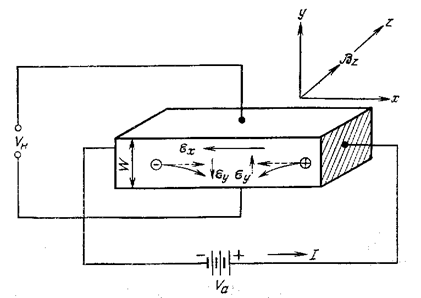
Внешнее поле Ex приложено вдоль оси x. Перпендикулярно ему (вдоль оси z) направлено магнитное поле Bz, а с верхнего и нижнего контактов снимается так называемое холловское напряжение VH. Для определенности будем считать образец дырочным (p-типа). Сила Лоренца qvx*B2 отклоняет дырки к нижней поверхности образца, где они частично накапливаются, что приводит к возникновению вертикального электрического поля Eу — холловского поля, которое компенсирует действие силы Лоренца на дырки и обеспечивает равенство нулю вертикального тока Jу. Холловское поле пропорционально плотности продольного тока Jx и напряженности магнитного поля Bz. Его величину находят, измеряя холловское напряжение VH: Ey=Vy/W=RHJxBz,
где RH—коэффициент Холла, определяемый выражениями
,
.
Параметр t — среднее время свободного пробега носителей. Его величина зависит от энергии носителей E. В частности, в полупроводниках со сферическими изоэнергетическими поверхностями 
при рассеянии на фононах и 
при рассеянии на ионизированных примесях. В общем случае можно считать что 
, где а и s— постоянные.
Для рассмотренных механизмов рассеяниякоэффициент r оказывается равным 3p/8 =1,18 при рассеянии на фононах и 315p/512 = 1,93 при рассеянии на ионизированных примесях.
Холловская подвижность mH определяется как произведение коэффициента Холла на проводимость:
.
Ее следует отличать от дрейфовой подвижности mn (или mp). Для полупроводников с ярко выраженным типом пооводимости(n>>p или р >> п) получаем
и 
.
Следовательно, в этих случаях из холловскнх измерений можно непосредственно определить и тип проводимости (электроны или дырки), и концентрацию носителей.
Перейти на страницу: 1 2 3 4 5