Стохастический резонанс
Для случая белого шума, параболических потенциальных ям и относительно высоких потенциальных барьеров скорость Крамерса дается законом Аррениуса:
 |
Рисунок 1 - Бистабильный потенциал под действием слабой периодической модуляции. Потенциал может иметь как "жесткую", так и "мягкую" форму. Частица, отмеченная шариком, может преодолеть потенциальный барьер At/o только в присутствии внешнего или внутреннего шума.
В присутствии периодической силы потенциальные ямы будут периодически колебаться (рис. 1), вероятности перехода также станут периодическими функциями времени, и выходной сигнал будет включать периодическую компоненту.
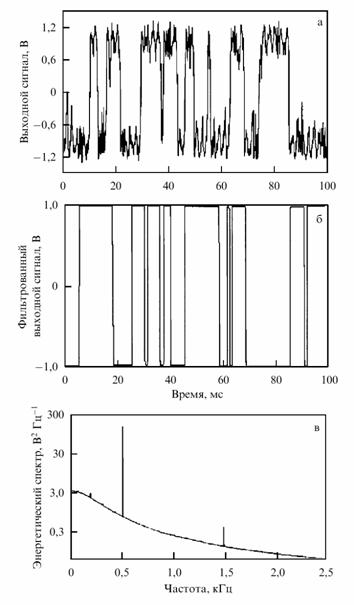
На рисунке 2 представлены сигналы на выходе бистабильной системы с учетом внутриямной динамики (а) и с учетом исключительно моментов времени пересечения барьера (приближение двух состояний) (б), а также спектр мощности (в) сигнала, показанного на графике (б).
Периодическая модуляция потенциала приводит к периодической модуляции как высоты потенциального барьера DU @ DU0 + Аsin(wt), так и вероятности перехода. В итоге в спектре мощности выходного сигнала регистрируется d-пик на частоте модуляции и ее нечетных гармониках (в случае симметричного потенциала). Предположим, что потенциальный барьер DU0, амплитуда и частота модуляции фиксированы. Частота Крамерса rk будет зависеть только от интенсивности шума D. При малой интенсивности шума время перехода чрезвычайно велико и намного превышает период сигнала модуляции. При высоком уровне шума за время одного периода сигнала система с высокой степенью вероятности совершит многократные переключения. Варьируя интенсивность шума, можно обеспечить режим, когда среднее время переходов через барьер близко к периоду сигнала модуляции. Переключения системы будут происходить в среднем в фазе с внешней периодической силой. Таким образом, варьируя интенсивность шума, можно настроить стохастическую бистабильную систему в режим максимального усиления сигнала модуляции и отношения сигнал/шум. Теоретические и экспериментальные исследования это подтвердили.
С понятием "шум" в обыденном сознании ассоциируется термин "помеха", наличие которой может только ухудшить функционирование любой системы. Хорошо известны классические проблемы радиофизики, связанные с ограничением чувствительности усилителей и конечностью ширины спектральной линии генераторов, что обусловлено воздействием естественных и технических шумов. В силу дискретности строения материи флуктуационные явления присущи всем реальным системам и принципиально неустранимы. Со времен Больцмана стала ясной ограниченность чисто детерминистского описания эволюционных процессов, и это ускорило развитие статистической физики. Основатели теории нелинейных колебаний также сознавали ограниченность детерминированного описания. Уже в 1933 г. ими был поставлен вопрос о статистическом рассмотрении динамических систем, что послужило основой для развития исследований в области статистической радиофизики.
Было установлено, что наличие источников шума в нелинейных динамических системах может индуцировать принципиально новые режимы функционирования, которые не могут быть реализованы в отсутствие шума, например, индуцированные шумом незатухающие колебания. Эффекты указанного типа получили название индуцированных шумом переходов. Многообразие и сложность типов таких переходов в нелинейных динамических системах вызвали постановку удивительных до недавнего времени вопросов: всегда ли воздействие шума приводит к ухудшению характеристик динамических систем и возможны ли случаи, когда действие шума вызывает увеличение степени упорядоченности движений в системе или улучшение ее рабочих характеристик? Исследования последних лет убедительно показали, что в нелинейных системах воздействие шума может индуцировать новые более упорядоченные режимы, приводить к образованию более регулярных структур, увеличивать степень когерентности, вызывать рост усиления и увеличение отношения сигнал/шум и т.д. Другими словами, шум в нелинейных системах может играть конструктивную роль, вызывая рост степени порядка в системе.
Одним из наиболее ярких и относительно простых примеров указанного типа поведения нелинейных систем при воздействии шума является эффект стохастического резонанса (СР). Эффект СР определяет группу явлений, при которых отклик нелинейной системы на слабый внешний сигнал заметно усиливается с ростом интенсивности шума в системе. При этом интегральные характеристики процесса на выходе системы, такие как коэффициент усиления и отношение сигнал/шум, имеют отчетливо выраженный максимум при некотором оптимальном уровне шума. В то же время энтропия как мера степени беспорядка достигает минимума, свидетельствуя о возрастании степени индуцированного шумом порядка.
Термин "стохастический резонанс" был введен в 1981 -1982 гг. на основе исследований модели бистабильного осциллятора, предложенной для описания периодичности в наступлении ледниковых периодов на Земле. Модель описывала движение частицы в симметричном двухъямном потенциале под действием периодической силы в условиях большого трения. Устойчивые положения частицы соответствовали ледниковому периоду и нормальному климату Земли. Периодическая сила соответствовала колебаниям эксцентриситета орбиты Земли. Расчеты показали, что реальная амплитуда периодический силы оказалась малой и не обеспечивала переключений системы из одного состояния в другое. Возможность переключений была достигнута путем введения дополнительной случайной силы, индуцирующей переходы через потенциальный барьер.
Перейти на страницу: 1 2 3 4 5 6