Стохастический резонанс
[Asinwt+x(t)]> P или < P.
Рассмотрим явление СР, используя концепцию нединамическою порогового эффекта. Временные диаграммы моделирования данного процесса получены с помощью пакета Microcap 7.0. Схема моделирования представлена на рисунке 3. Она включает в себя два генератора сигналов: гармонического сигнала и шума. С них сигнал поступает на сумматор и далее на компаратор. На инвертирующий вход компаратора подается постоянное напряжение, определяющее уровень порога срабатывания. На выходе компаратора находится фильтр низких частот, состоящий из RC-цепи.
 |
Рисунок 3 – Схема моделирования стохастического резонанса в пороговой системе
 |
Рисунок 4 – График регулярного сигнала и шума
Всякий раз, когда уровень порога пересекается в одном направлении, генерируется импульс стандартной формы. Процесс пересечений порога порождает во времени случайную последовательность импульсов на выходе компаратора, как это показано на рисунке 5.
 |
Рисунок 5 – График сигнала на выходе порогового элемента
На рисунке 6 находится амплитудный спектр данной последовательности импульсов, полученный с помощью быстрого преобразования Фурье. На фоне шума четко видна гармоника с частотой сигнала.
 |
Для того чтобы получить сигнал, наиболее похожий на исходный, необходимо отфильтровать высокочастотные составляющие спектра. Для этих целей используется фильтр низких частот в виде RC-цепи. Временная диаграмма сигнала на выходе фильтра и его амплитудный спектр представлены на рисунке 7.
Рисунок 7 – График выходного сигнала и его амплитудного спектра
На данном графике видно , что на выходе фильтра получился сигнал с искажениями, но совпадающий по форме и частоте со входным сигналом. Для наилучшего восстановления сигнала на выходе, необходимо найти параметры схемы и сигналов, соответствующие максимальному отношению энергии сигнала к энергии шума.
Для этого необходимо найти оптимальный уровень шума, который добавляется к сигналу. Поэтому будем считать порог срабатывания компаратора и амплитуду входного сигнала величинами постоянными, а находить будем зависимость отношения энергии сигнала к энергии шума на выходе компаратора в зависимости от уровня шума на входе.
Моделирование будем производить в пакете Mathcad 2000. Зададим шум на входе как сумму нескольких случайных величин с равномерным распределением плотности вероятности. В результате мы получим случайный процесс, похожий по свойствам на гауссовский белый шум, так как по центральной предельной теореме распределение плотности вероятности суммы большого количества независимых случайных величин близко к нормальному распределению.
Определим зависимость сигналов на входе и выходе порогового элемента условием
где x(t) – сигнал на входе,
y(y) – сигнал на выходе,
P – порог срабатывания порогового элемента.
Тогда во все моменты времени, в которые входной сигнал выше порогового, на выходе будет уровень единицы.
 |
В результате моделирования были получены графики для трех частот входного сигнала: w0=4 кГц, w0=16кГц, w0=64кГц. Порог срабатывания и амплитуда входного сигнала постоянны. Уровень шума показан как отношение его амплитуды к амплитуде сигнала. Зависимости представлены на рисунках 8-10.
 |
Рисунок 8 – Результаты моделирования эффекта СР для частоты входного сигнала w0=4кГц
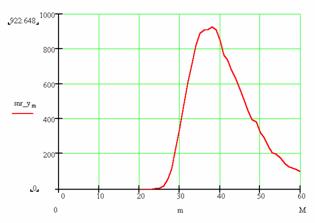
Рисунок 9 - Результаты моделирования эффекта СР для частоты входного сигнала w0=16кГц
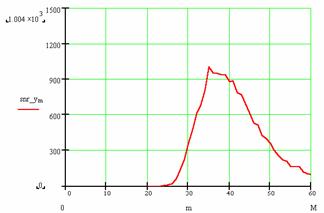
Рисунок 10 - Результаты моделирования эффекта СР для частоты входного сигнала w0=64кГц
4 Синхронизация стохастических систем
Применение теории линейного отклика даст хорошие результаты, вскрывающие физический механизм явления СР. Возникает вопрос: почему? Ведь все стохастические системы, демонстрирующие эффект СР, принципиально нелинейны! Дело в том, что основные нелинейные свойства стохастических систем учитываются в том или ином приближении при определении корреляционной функции не возмущенной системы. Нелинейность системы проявляется в зависимости корреляционной функции от интенсивности шума D, в результате чего от D зависит и восприимчивость. Ограничения теории линейного отклика ведут к требованию малости амплитуды сигнала возмущения. Отказ от этого условия переводит проблему в класс принципиально нелинейных, и теория линейного отклика становится неприменимой.
Перейти на страницу: 1 2 3 4 5 6