Стохастический резонанс
Одним из важных нелинейных эффектов, сопровождающих эффект СР, является синхронизация. Синхронизация стохастических систем, не имеющих собственных периодических компонент во временных реализациях процесса, — явление нетривиальное. Однако недавно были открыты эффекты как внешней, так и взаимной стохастической синхронизации. Очки для зрения купить оправы для медицинских очков.
4.1 Синхронизация стохастического бистабильного осциллятора
Для рассмотрения эффекта синхронизации стохастических систем обратимся к результатам исследований неавтономного генератора Ван дер Поля — классической автоколебательной системы с предельным циклом, находящейся под воздействием периодической силы и флуктуации. Как известно, наличие шума ведет к флуктуациям амплитуды и фазы колебаний. В результате разность фаз колебаний генератора и внешней гармонической силы ф(t)=f(t)-y(t) также будет флуктуировать. В приближении постоянной амплитуды медленная динамика разности фаз ф(t) описывается следующим СДУ:
f=D - е*sinf+x(t)
где D=W-W0 есть разность частот генератора и внешней силы (расстройке по частоте), е – параметр нелинейности, x(t) – гауссов шум. Разность фаз ф(t) совершает броуновское движение в передемпфированном осцилляторе c наклонным периодическим потенциалом U(ф) = -Dф-e* cos ф. При малом уровне шума разность фаз флуктуирует длительное время внутри одной из потенциальных, ям (эффект захвата фаз) и редко совершает перескажи через потенциальный барьер (нарушение синхронизации),
В отличие от классической синхронизации детерминированных систем, в случае стохастических колебаний необходимо использовать понятие "эффективной синхронизации" с учетом ограничений на флуктуации фазы, частоты и отношения сигнал/шум. Будем использовать наиболее жесткое определение эффективной синхронизации: система функционирует в режиме эффективной синхронизации, если среднее время захвата фазы много больше периода внешней гармонической силы. Количественной мерой степени эффективной синхронизации будет коэффициент эффективной диффузии разности фаз Deff.
Можно показать, что Deff пропорциональна средней скорости r перехода через барьер
Deff = 4*p2*r
и обратно пропорциональна среднему интервалу времени захвата разности фаз :
(Т) = н2p/W0. n>> 1.
Таким образом, критерий эффективной синхронизации можно определить как:
Deff<2*p*W0/n n>>1 .
Эффект воздействия шума на синхронизируемый автогенератор хорошо изучен: с ростом интенсивности шума условия синхронизации ухудшаются, так что коэффициент эффективной диффузии возрастает с увеличением интенсивности шума. Области синхронизации в пространстве параметров системы сужаются с ростом шума. Иными словами, шум действует против синхронизации, внося беспорядок (стохастическую диффузию фазы). Как мы увидим из дальнейшего, в системах, демонстрирующих СР, шум играет принципиально иную роль.
4.2 Внешняя стохастическая синхронизация триггера Шмитта
При изучении синхронизирующего действия внешнего периодического сигнала на стохастические бистабильные системы основной интерес представляет глобальная динамика переходов между метастабильными состояниями. Поэтому для исследований синхронизации удобно использовать идеальную бистабильную систему - триггер Шмитта.
Проведем моделирование эксперимента измерения средней частоты от интенсивности шумового сигнала. На триггер Шмитта с порогом срабатывания DU=200мВ будем подавать шумовой сигнал и периодический сигнал с частотой 100Гц. При слабом сигнале зависимость средней частоты от интенсивности шума не зависит от сигнала и экспоненциально возрастает. С увеличением амплитуды сигнала зависимость средней частоты от интенсивности шума качественно иная: появляется область значений интенсивности шума, в котором средняя частота переключений практически не меняется сростом шума и в пределах погрешности моделирования остается равной частота сигнала. Наблюдается эффект захвата частоты. На рисунке 11 представлены графики зависимости переключений триггера Шмитта от интенсивности шума с амплитудой сигнала А=0мВ, А=50мВ и А=100мВ.
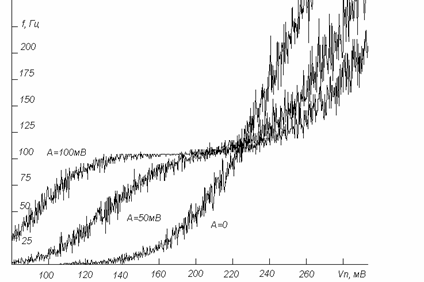 |
Рисунок 11 – Зависимость частоты выходного сигнала триггера Шмитта от интенсивности шума для различных значений амплитуды А сигнала.
Из приведенного примера следует, что внешний периодический сигнал достаточной амплитуды синхронизирует стохастическую динамику процессов. Хотя амплитуда сигнала находится за приделами применимости теории линейного отклика, она остается малой настолько, что в отсутствии шума переключений не происходит. Шум таким образом, является необходимым компонентом рассматриваемого явления. Это явление сопровождается захватом мгновенной фазы и средней частоты.
5 Стохастический резонанс и количественная оценка восприятия информации
Практически во всех экспериментах по изучению СР используются методы компьютерного анализа сигналов на входе и выходе изучаемых систем, с помощью которых обосновывается усиление (или увеличение информации) при действии оптимального уровня шума. Можно попытаться протестировать общий интегральный эффект в каких-либо поведенческих, т.е. психологических, экспериментах с человеком. Другими словами, можно заменить сложное программное обеспечение обработки данных на ЭВМ на человеческое восприятие (интерпретацию). Такие эксперименты были разработаны и проведены специально для исследования способности человека воспринимать зрительно информацию на фоне воздействия шума. Будет ли визуально воспринимаемая информация зависеть от интенсивности шума нелинейным образом, подобно эффекту СР? Возможно ли ввести количественный критерий оптимальности зрительного восприятия информации? Ответ на эти вопросы дан и является утвердительным.
Произвольно выбранную фотографию оцифруем на 256 уровней серого цвета и выведим на экран в качестве изображения 200*200 точек. Затем поместим ее ниже порогового уровня, так что бы ее не было видно. К подпороговому уровню добавим гауссов шум с нулевым средним, который действовал на каждый дискретный элемент независимо (источники шума в каждом элементе не коррелированны). Если в каком-либо конкретном пикселе преодолевался пороговый уровень-то он становится черного цвета. При малом уровне шума лишь небольшое количество точек появляется на экране и картинку не возможно распознать. Если шум слишком большой распознавание образа также невозможно. Однако всегда существует некоторое оптимальное значение интенсивности шума, когда информация о картинке максимальная и ее можно воспринять. Один из примеров приведен на рисунках , из которого видно, что наиболее отчетливо воспринимается изображение на рисунке , когда интенсивность внешнего шума оптимальна. Эффект восприятия картинки на самом деле динамический, ведь человеческий глаз обладая определенной инерцией более четко воспринимает те области изображения где появление черных точек больше белых. Этот эффект можно использовать для создания примитивного фильтра восстановления изображения.
Перейти на страницу: 1 2 3 4 5 6
