Пародоксы теории относительности
3. Изотропность предполагает также симметричность пространства. В силу же симметрии ничто не должно измениться в формулах преобразования, если изменить знаки 
и 
, т.е. одновременно изменить направление оси и направление движения системы 
. Следовательно, 
(d) Сравнивая эти уравнения с предыдущими (
) получаем: 
. Вместо 
удобно ввести другую функцию 
, так, чтобы 
выражалось через 
и
посредством соотношения 
Согласно этому соотношению, - симметричная функция. Используя это соотношение, преобразования (d) можно записать в виде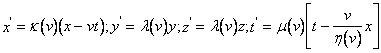 
(e), причем все входящие в эти формулы коэффициенты 
суть симметрии функции .
4. В силу принципа относительности обе системы, "движущаяся" и "неподвижная", абсолютно эквивалентны, и поэтому обратные преобразования от системы 
к
должны быть тождественно прямым от к. Обратные преобразования должны отличаться лишь знаком скорости , т.к. системадвижется относительно системывправо со скоростью , а система движется относительно системы (если последнюю считать неподвижной), влево со скоростью 
. Следовательно, обратные преобразования должны иметь вид 
. (f) Сравнивая эти преобразования с (e), получаем 
. Но в силу симметрии получаем, что 
, т.е. 
. Очевидно, имеет смысл лишь знак (+), т.к. знак (–) давал бы при 
перевернутую по 
и 
систему. Следовательно 
. Замечая, что коэффициенты 
- тоже симметричные функции , первое и последнее уравнение из (e) и (f) можно записать в виде: А) 
, а) 
, В) 
, в) 
. Умножая А) на , В) на 
и складывая, получим 
. Сравнивая это выражение с а), получаем 
. Откуда имеем 
Следовательно, извлекая квадратный корень и замечая, что знак (-) так же, как и для 
, не имеет смысла, получаем 
. Итак преобразования приобретают вид: 
(g) или ,подробнее: 
,(h) где - неизвестная пока функция .
5. Для определения вида обратимся вновь к принципу относительности. Очевидно, что преобразования (g) должны быть универсальными и применимыми при любых переходах от одних систем к другим. Таким образом, если мы дважды перейдем от системык и от к 
, то полученные формулы, связывающие координаты и время в системе с координатами и временем в, должны также иметь вид преобразований (g). Это вытекающее из принципа относительности требование, в совокупности с предыдущими требованиями обратимости, симметрии и т.д. означает, что преобразования должны составлять группу.
Перейти на страницу: 1 2 3 4 5 6 7 8 9