Тунельные и барьерные эффекты
Похожий эффект проявляется в туннельных диодах, в которых зоны наклонены благодаря полупроводникам р- и n-типа по обе стороны от границы их соприкосновения. Туннелирование осуществляется благодаря тому, что в зоне, куда переходит носитель заряда, имеется конечная плотность незанятых состояний.
Благодаря Туннельному эффекту возможен электрический ток между двумя металлами, разделёнными тонкой диэлектрической перегородкой. Эти металлы могут находиться как в нормальном, так и в сверхпроводящем состоянии. В последнем случае может иметь место Джозефсона эффект.
Туннельный эффект. обязаны такие явления, происходящие в сильных электрических полях, как автоионизация атомов и автоэлектронная эмиссия из металлов. В обоих случаях электрическое поле образует барьер конечной прозрачности. Чем сильнее электрическое поле, тем прозрачнее барьер и тем сильнее электронный ток из металла. На этом принципе основан сканирующий туннельный микроскоп - прибор, измеряющий туннельный ток из разных точек исследуемой поверхности и дающий информацию о характере её неоднородности.
Туннельный эффект. возможен не только в квантовых системах, состоящих из одной частицы. Так, например, низкотемпературное движение дислокаций в кристаллах может быть связано с туннелированием конечной части дислокации, состоя из многих частиц. В такого рода задачах линейную дислокацию можно представить как упругую струну, лежащую первоначально вдоль оси у в одном из локальных минимумов потенциала V(x, у). Этот потенциал не зависит от у, а его рельеф вдоль оси х представляет со последовательность локальных минимумов, каждый из которых находится ниже другого на величину, зависящую от приложенного к кристаллу механического напряжения. Движение дислокации под действием этого напряжения свода к туннелироваиию в соседний минимум определенного отрезка дислокации с последующим подтягиванием туда оставшейся её части. Такого же рода туннельный механизм может отвечать за движение волн зарядовой плотности в диэлектрике Пайерлса.
Для расчётов эффектов туннелирования таких многорамерных квантовых систем удобно использовать квазикласическое представление волновой функции в виде ψ~exp(iS), S—классическое действие системы. Для туннельного эффекта. существенна мнимая часть S, определяющая затухание волновой функции в классически недоступной области. Для её вычисления используется метод комплексных траекторий.
Квантовая частица, преодолевающая потенциальный барьер может быть связана с термостатом. В классической механике это соответствует движению с трением. Тем самым, ; описания туннелирования необходимо привлечение теории, получившей название диссипативной квантовой механики. Такого рода соображения необходимо использовать для объяснения конечного времени жизни токовых состояний контактов Джозефсона. В этом случае происходит туннелирование эффекта. квантовой частицы через барьер, а роль термостата играют нормальны электроны.
§ 1. Прохождение микрочастиц через потенциальные барьеры.
Постановка проблемы и простейшие случаи.
Если мы имеем две области пространства, в которых потенциальная энергия частицы меньше, нежели на поверхности, разделяющей эти области, то мы говорим, что области разделены потенциальным барьером.
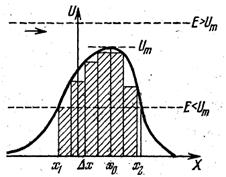
Простейшим примером потенциального барьера может служить барьер в одном измерении, изображенный на рис.1. По оси ординат отложена потенциальная энергия U (х) в функции координаты частицы х. В точке х0 потенциальная энергия имеет максимум Um. Все пространство - ∞ < Х < + ∞ делится в этой точке на две области; х < х0 и х > х0 , в которых U<Um. Значение термина «потенциальный барьер» сейчас же выяснится, если мы рассмотрим, движение частицы в поле U (х) на основе классической механики. Полная энергия частицы E равна
![]() (1)
(1)
где р —импульс частицы, а μ – её масса. Решая (1) относительно импульса, получим
![]() (2)
(2)
Знаки ± следует выбрать в зависимости от направления движения частицы. Если энергия частицы Е больше «высоты» барьера Um, то частица беспрепятственно пройдет барьер слева направо, если начальный импульс р>0, или в противоположном направлении, если начальный импульс р < 0.
Допустим, что частица движется слева, имея полную энергию Е, меньшую U т. Тогда в некоторой точке xt потенциальная энергия U (х1)=Е, p(x1)=0, частица остановится. Вся ее энергия обратится в потенциальную, и движение начнется в обратном порядке: х1 есть точка поворота. Поэтому при E<.Um частица, движущаяся слева, не пройдет через область максимума потенциала (х = х0) и не проникнет во вторую область х > х0 Подобным же образом, если частица движется справа налево, имея Е < Um , то она не проникнет в область за второй точкой поворота х2,
|
|
|
|
Рис. 1.1. Потенциальный барьер в одном измерении. |
Рис. 1.2. Самый простой потенциальный барьер |
в которой U(x2)=E (рис.1). Таким образом, потенциальный барьер является «непрозрачной» перегородкой для всех частиц, энергия которых меньше Um (напротив, он «прозрачен» для частиц, обладающих энергией Е >Um). Этим и разъясняется название «потенциальный барьер».
Совсем иначе протекают явления вблизи потенциальных барьеров, если речь идет о движениях микроскопических частиц в микроскопических полях, т. е. о движениях, при рассмотрении которых нельзя игнорировать квантовые эффекты. В этом случае, как мы сейчас увидим, в противоположность выводам классической механики, частицы с энергией Е, большей высоты барьера Um, частично отражаются от барьера, а частицы с энергией, меньшей Um, частично проникают через барьер.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11