Концепция современного естествознания
Для перехода из одной инерциальной системы отсчета в другую Галилей ввел преобразования, которые теперь называют преобразованиями Галилея. Рассмотрим следующую ситуацию. Пусть у нас имеется инерциальная система отсчета, положение тел в которой задается декартовыми координатами. Например, точка А на рис. 10.3. https://ak-39.ru резюме Аварийный комиссар в Калининграде.
Кроме системы координат XYZ (ее обычно обозначают К), может быть и другая инерциальная система координат, например, X’Y’Z’ (назовем ее К’). Инерциальная система координат К’ движется с постоянной скоростью u относительно системы К. Пространство изотропное, в нем не существует выделенного направления, поэтому удобно выбрать направление оси OX совпадающим с направлением скорости u. Т.е. система К’ движется вдоль оси OX системы отсчета К.
y’
y
v
О’ x’
z’ O x
z
x
Рис.10.3
Положение точки А в системе К задается вектором r(x,y,z) или его проекциями на оси OX, OY и OZ, которые равны, соответственно, x, y и z. Положение той же точки в системе К’ задаются координатами x’, y’ и z’. Связь между x, y, z и x’, y’, z’ дается преобразованиями Галилея:
Дополнительно к преобразованиям координат введено преобразование времени. Одинаковость хода часов в разных инерциальных системах отсчета соответствует концепции дальнодействия, рассмотренной выше.
Введем понятие инварианта и инвариантности. Инвариантность означает независимость, неизменность относительно каких-либо физических условий. В математике под инвариантностью понимается неизменность величины относительно каких-либо преобразований. Рассмотрим, какие параметры не меняются при преобразованиях Галилея, т.е. являются инвариантами этих преобразований.
Первый из этих параметров - время. При переходе от одной инерциальной системы отсчета к другой не меняется как само время t=t’, так и длительность какого-либо события 
:
.
Помимо времени, неизменным остается расстояние между двумя точками. Обозначим расстояние между точками А и В через 
в системе K и 
в системе K’. Координаты этих точек, соответственно, 
в системе K и 
в системе К’. Расстояние между точками определяется их координатам по теореме Пифагора:
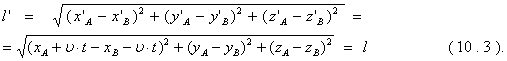
Продифференцируем по времени соотношения (10.1) и получим преобразования Галилея для скоростей:
Из этих формул видно, что при переходе от системы К к К’ изменится лишь проекция скорости на ось OX, вдоль которой движется система К’, проекции скорости на направления других осей сохранятся. Продифференцируем эти выражения по времени еще раз и получим закон преобразования ускорений при переходе из одной инерциальной системы отсчета в другую:
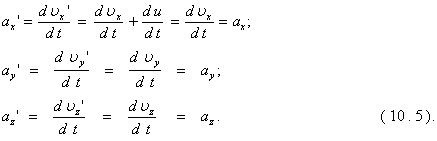
Из этих выражений видно, что все три проекции ускорения на оси координат остаются неизменными при переходе из системы отсчета К в К’. Таким образом, ускорение тоже является инвариантом преобразований Галилея.
Закон сохранения массы был сформулирован уже после Галилея и Ньютона. Но, для полноты картины, добавим, что в классической механике масса тела не зависит от выбора системы отсчета и также является инвариантом преобразований Галилея.
10.3. Законы классической механики и их инвариантность относительно преобразований Галилея.
Создание основ классической механики завершается трудами И.Ньютона, сформулировавшего основные законы механики и открывшего закон всемирного тяготения. Классическая механика Ньютона базировалась на работах Галилея, Декарта, Паскаля, Гука и многих других.
Раздел механики, в котором изучаются причины движения тел, т.е. силы, вызывающие их движение, называется динамикой. Основные законы механики, сформулированные Ньютоном дошли почти без изменений до наших дней. Они известны из школьного курса физики. Напомним их.
Первый закон Ньютона. Всякое тело в инерциальной системе отсчета сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
Второй закон Ньютона. Ускорение тела прямо пропорционально сумме сил, действующих на него и обратно пропорционально его массе. Запишем этот закон в векторной форме с учетом кинематических соотношений
В этих формулировках мы использовали понятие импульса или количества движения P = m×u, которое было введено Декартом. Закон Ньютона, записанный в виде (10.6.а) или (10.6.б) с математической точки зрения имеет вид дифференциального уравнения, т.е. уравнения в котором значение функции связывается со значением ее производной. Любая из формулировок (10.6.а,б) второго закона Ньютона называется основным уравнением динамики. Решение этого уравнения является основной задачей динамики. Основная задача динамики может быть поставлена в форме прямой и обратной задачи. В прямой задаче требуется по известному закону движения тела r(t) найти действующие на это тело силы. В обратной задаче по известной зависимости действующих сил от времени SF(t) требуется найти закон движения тела r(t). Различные формулировки (10.6) могут немного менять постановку основной задачи, как прямой, так и обратной. Однако, прямая задача всегда математически сводится к дифференцированию, а обратная - к интегрированию. Очевидно, что решение обратной задачи динамики должно быть значительно более трудоемким, чем прямой. Отметим также, что для решения обратной задачи требуется знать начальные условия, которых в зависимости от постановки задачи (в форме 10.6.а или 10.6.б) должно быть задано либо столько же, сколько и степеней свободы системы, либо вдвое больше.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21