Концепция современного естествознания
Аbc O
C Eпот(С) Aco
Рис. 11.3
Оказалось доказанным следующее утверждение: работа, совершаемая при перемещении тела в поле консервативных сил из точки (b) в точку (c), равна разности потенциальных энергий тела в точках (b) и (c). Однако, эта же работа равна разности кинетических энергий в точке (с) и (b).
Получилось, что сумма кинетической и потенциальной энергии тела, которая называется полной механической энергией тела, оказалась неизменной. Тоже самое справедливо и для системы механических тел. Получившееся утверждение носит название закона сохранения механической энергии: полная механическая энергия изолированной системы в которой действуют консервативные силы остается неизменной.
Между консервативными силами и потенциальной энергией должна быть связь, поскольку потенциальная энергия вводится только в поле консервативных сил. Найдем эту связь для простейшего случая, когда потенциальная энергия зависит только от одной координаты. Примером может служит потенциальная энергия вблизи поверхности Земли, к нему и обратимся. Пусть ось (oy) направлена вертикально вверх и имеет ноль на поверхности Земли. Тогда потенциальная энергия зависит только от координаты y и равна: 
где m - масса тела, 
ускорение свободного падения вблизи поверхности Земли. Возьмем частную производную по координате y от левой и правой частей равенства: 
. Справа стоит сила тяжести, которая направлена вверх, т.е. против оси (oy). По-видимому, производной, стоящей в левой части равенства тоже можно приписать направление; ее проекция на ось (oy) будет равна 
. В случае, когда действующая сила имеет проекции на все координатные оси, можно записать аналогичные выражения и для проекций на другие оси.
Для силы, таким образом, справедливо выражение:
.
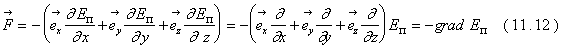В формуле (11.12) введен вектор градиента потенциальной энергии. Определение этого понятия дается в разделе математики, который называется теорией поля. Отметим лишь некоторые свойства этого вектора. Особенность его состоит в том, что вдоль координатных осей нужно откладывать не числа, а математические операции дифференцирования по соответствующей координате. За градиентом обязательно должна стоять скалярная функция, к которой он применяется. Градиент потенциальной энергии имеет направление, в котором потенциальная энергия увеличивается быстрее всего, и величину, равную скорости этого увеличения, если двигаться в этом направлении.
Из сказанного следует, что силы поля заставляют тело двигаться в направлении минимума потенциальной энергии. Все естественные процессы стремятся привести систему к минимуму потенциальной энергии. Этот вывод справедлив не только для механики, но и для других разделов физики и естествознания.
Мы рассмотрели взаимопревращение кинетической и потенциальной энергий в поле консервативных сил. Что происходит, если действуют неконсервативные силы. Мы знаем, что, если телу сообщит скорость (сообщить кинетическую энергию)и пустить двигаться, например, по поверхности земли, оно остановиться за счет сил трения. Его потенциальная энергия не изменится, а кинетическая станет равной нулю, когда оно остановиться. Для ответа на вопрос, во что перешла кинетическая энергия, необходимо ввести еще один вид энергии- внутреннюю энергию. Определим внутреннюю энергию Евн как сумму кинетических и потенциальных энергий частиц (атомов), составляющих тело:
Евн = S(Еiпот+Еiкин) (11.13)
Здесь N -число частиц, i -номер частицы. Параметром, характеризующим внутреннюю энергию является температура тела Т0К, выраженная в градусах Кельвина. Чем больше температура тела, тем с большей скоростью двигаются атомы и тем самым больше внутренняя энергия. Численно внутренняя энергия равна:
Евн=(М/m)C Т0 (11.14)
М - масса тела, m -молярная масса (численно равная атомному или молекулярному весу составляющих атомов),С -теплоемкость, равная энергии, которую нужно передать одному килограмму-молю, чтобы нагреть его на 1 градус Цельсия или Кельвина. Изменение внутренней энергии при переходе системы из состояния 1 в состояние 2 пропорционально изменению температуры тела : Евн(2)-Евн(1) = DU = (M/m)C DT0.
Сумму кинетической, потенциальной и внутренней энергий системы принято называть полной энергией Е. В рассмотренном нами примере с останавливающемся телом кинетическая энергия тела переходит во внутреннюю энергию, т.е. идет на нагревание системы.
С учетом вышесказанного мы можем сформулировать закон сохранения полной энергии системы: Полная энергия изолированной системы остается постоянной. Мы теперь не конкретизируем, какие силы (консервативные или неконсервативные) действуют в этой системе. Работа в системе, совершаемая за счет потенциальной энергии, может переходить и в кинетическую энергию системы, и во внутреннюю энергию. При увеличении внутренней энергии система нагревается.
12. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ.
12.1 Постулаты теории относительности.
К концу прошлого века Д.К.Максвеллом (1831-1879) были сформулированы основные законы электричества и магнетизма в виде системы дифференциальных уравнений, которые описывали постоянные и переменные электрические и магнитные поля. Решения системы уравнений Максвелла описывали всю гамму поведений электромагнитных полей в пространстве и времени. Из системы уравнений Максвелла следовало, что переменные электрические и магнитные поля могут существовать только в форме единого электромагнитного поля, которое распространяются в пространстве после возникновения с постоянной скоростью, равной скорости света в вакууме - с.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21