Концепция современного естествознания
На вопрос о том, в какой среде распространяется это поле, теория Максвелла ответа не давала. Ключевым моментом теории Максвелла являлось то, что уравнения Максвелла были неинвариантны относительно преобразований Галилея. Это означало, что при переходе с помощью преобразований Галилея из одной инерциальной системы отсчета в другую, уравнения меняли свой вид. Это обозначало, что преобразования Галилея нельзя было применять при описании электрических и магнитных явлений.
Строгое математическое доказательство неинвариантности уравнений Максвелла относительно преобразований Галилея достаточно сложно. Поэтому, проиллюстрируем этот факт на простом и наглядном примере. Для этого потребуется вспомнить, какие силы действуют на движущиеся заряды в электрических и магнитных полях.
Пусть два одноименных заряда летят с одинаковой скоростью u в направлении оси (ox), как это показано на рис.12.1. В неподвижной системе отсчета заряды будут создавать электрические и магнитные поля, и, следовательно, будут находиться в полях друг друга. Электрическое поле воздействует на заряд силой Кулона, магнитное - силой Лоренца. Напомним формулы для вычисления этих сил для случая, приведенного на рисунке.
Здесь B1 - магнитная индукция, создаваемая первым зарядом в точке, где находится второй. Сила Кулона для одноименных зарядов всегда является силой отталкивания, а сила Лоренца в данном случае является силой притяжения. Таким образом, в неподвижной системе отсчета величина силы взаимодействия равна: F = FK - FЛ.
Если перейти к системе отсчета, движущейся вдоль оси (ох) со скоростью u вместе с зарядами, то в ней заряды окажутся неподвижными, и сила Лоренца не возникнет. Таким образом, силы взаимодействия зарядов в различных инерциальных системах отсчета окажутся разными. Следовательно и поведение частиц ,их движение во времени, будет разным в зависимости от того, в какой инерциальной системе координат мы рассматриваем это движение. Естественно, что это абсурд и отсюда сделаем вывод, что к движущимся зарядам, законы движения и взаимодействия которых описываются уравнениями Максвелла, нельзя применять принцип относительности Галилея, т.е. преобразования Галилея.
q
v
q v
O X
Рис. 12.1
Вторым этапом в становлении специальной теории относительности стал опыт А.А.Майкельсона (1852-1931), проведенный в 1881 году. В опыте определялась скорость света в различных движущихся системах отсчета. Уже говорилось, что по теории Максвелла электромагнитные волны должны распространяться со скоростью в вакууме - с. Встал вопрос, в какой инерциальной системе отсчета это происходит. Если таковой считать систему отсчета, связанную с неподвижными звездами, то скорость нашей планеты относительно них u = 30 км/с. Эта скорость большая и сравнимая со скоростью света с.
Майкельсон экспериментально определял скорость света в разных системах отсчета, а именно, он измерял скорость света, идущего в двух противоположных относительно Земли направлениях. В соответствии с преобразованиями Галилея и положениями классической механики, скорости света в этих системах отсчета должны были бы отличатся на величину 2u.
Результаты эксперимента Майкельсона однозначно показали, что скорость света не зависит от выбора системы отсчета и всегда равна с. Т.е. было установлено, что электромагнитные волны во всех инерциальных системах отсчета распространяются с одинаковой скоростью с=3×108 м/с. Эксперименты, подобные опыту Майкельсона повторялись неоднократно со все возрастающей точностью. На сегодняшний день можно утверждать, что скорость в различных системах отсчета одинакова с точностью порядка нескольких мм/с.
В 1904-м году голландский физик Х.А.Лоренц (1853-1928) вывел преобразования для перехода из одной инерциальной системы отсчета в другую, отличные от преобразований Галилея. Система уравнений Максвелла была инвариантна относительно этих преобразований. Преобразования касались и координат, и времени.
Обозначим координаты и время некоторого события (например положения материальной точки в пространстве) в инерциальной системе отсчета К через x, y, z, t, а в другой инерциальной системе отсчета К’ через x’,y’,z’,t’. Системы отсчета выбраны так, чтобы их координатные сетки начальный момент времени t=t’=0 совпадали, а в дальнейшем система К’ двигалась относительно системы К со скоростью u вдоль ее оси (ox). Преобразования Лоренца имеют вид:
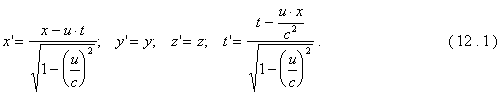. Сразу можно сказать, что при 
преобразования Лоренца переходят в преобразования Галилея. Т.е. преобразования Галилея являются частным случаем преобразований Лоренца при малых скоростях движения.
Анализируя сложившееся положение А.Эйнштейн разработал новую механику больших скоростей, называемую сейчас релятивистской механикой или специальной теорией относительности. В основе этой теории лежат два постулата.
Согласно первому постулату скорость распространения света во всех инерциальных системах координат одинакова и равна скорости распространения света в вакууме - с. Этот постулат утверждает эквивалентность инерциальных систем отсчета относительно скорости света.
Второй постулат заключается в том, что все физические законы и явления формулируются и протекают одинаково во всех инерциальных системах отсчета, т.е. инвариантны относительно преобразований Лоренца.
Базируясь на этих постулатах, Эйнштейн разработал теорию движения систем при любых скоростях, вплоть до скоростей света. В рамках теории относительности получены выводы, казалось бы противоречащие законам классической механики. Однако, все выводы этой теории подтверждены экспериментально с высокой точностью.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21