Концепция современного естествознания
Основное уравнение динамики движения релятивистской частицы имеет вид, схожий с основным уравнением движения классической динамики: 
однако, при дифференцировании по времени правой части нужно учесть, что релятивистская масса не есть постоянная величина. Отметим, что классическая формулировка второго закона Ньютона 
несправедлива даже с релятивистской массой.
Уравнения динамики релятивистской частицы (12.5-12.7) нашли блестящее подтверждение уже в 30-х годах нашего века при разработке первых ускорителей электронов, которые были названы бетатронами. На бетатронах электроны ускорялись в переменных электрических полях и приобретали скорость, сравнимую со скоростью света. Тогда то и было обнаружено, что масса частицы и траектория ее движения зависят от скорости в полном соответствии с формулами (12.5-12.7).
Уравнения релятивистской динамики позволили Эйнштейну найти связь массы и энергии тела. Попробуем вслед за ним найти количественной соотношение между этими величинами. Для этого преобразуем уравнение (12.6):
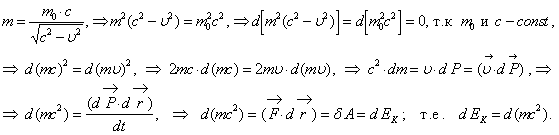Если дифференциалы величин равны, то сами величины могут различаться на постоянную величину: 
. Значение этой константы можно найти из условия, что при 
, выражение для кинетической энергии должно стремиться к 
Значение ее окажется равным 
. Таким образом, получаем релятивистское выражение для кинетической энергии: 
.
Отметим, что классические выражения для кинетической энергии, как 
неприменимы, даже если в них подставить релятивистские массы.
Второе слагаемое в этом выражении имеет смысл энергии покоя, внутренней энергии тела, энергии связанной с самим фактом существования тела и наличием у него массы в неподвижном состоянии. Сумма кинетической энергии и энергии покоя называется полной энергией тела. Выражение для полной энергии можно получить из формулы (12.9).
.
Мы получили самую известную формулу 20-го века, которая устанавливает количественную связь между энергией и массой. Ее можно трактовать следующим образом. Между полной энергией системы Е и ее массой m существует связь, определяемая формулой (12.10). Энергия при определенных условиях может переходит в массу, а масса - в энергию. Однако, понятие энергии не сводится только к массе и наоборот, масса не сводится только к энергии. Тем самым установлена связь между мерой количества материи - массой и мерой движения материи - энергией. Эта связь является отражением факта, что материя без движения, также, как и движение без материи не существует.
Рассмотрим пример, в котором полученная формула играет определяющую роль. При делении ядра урана образуется два более легких ядра. При этом масса ядра урана больше суммы масс образовавшихся ядер на величину Dm. Дефект массы Dm не исчезает, а переходит в кинетическую энергию осколков - дочерних ядер: DЕ=Dm×c2. Кинетическая энергия этих осколков - и есть та энергия, которая высвобождается при взрыве атомной бомбы или в атомном реакторе.
13. ЗАКОНЫ СОХРАНЕНИЯ
13.1 Законы сохранения, как отражение симметрии процессов преобразования.
Идея сохранения, следствием которой являются законы сохранения, появилась сначала как чисто философская догадка о наличии стабильного, неизменного в вечно изменяющемся мире. Еще античные философы-материалисты пришли к понятию материи - неучтожимой и несотворимой основы всего существующего. С другой стороны, наблюдения постоянных изменений в природе приводило к представлению о вечном движении материи как важнейшем ее свойстве и, как следствие этого, к изменяемости одних и неизменности других свойств материи.
В этом разделе мы рассмотрим законы сохранения как отражение некоторых операций, вводимых в физике. Напомним, что законами сохранения называются те закономерности, согласно которым численные значения некоторых параметров или величин не меняются со временем в любых процессах или в определенном классе процессов.
Важнейшими законами сохранения, справедливыми для любых изолированных систем, являются законы сохранения энергии, импульса, момента импульса и электрического заряда.
Полное описание физической системы возможно только с использованием динамических законов. Так описание движения материальной точки возможно с использованием законов динамики или законов Ньютона. Однако во многих случаях динамические законы системы либо неизвестны вообще, либо они настолько сложны, что не поддаются анализу. В таких случаях законы сохранения позволяют сделать заключения о характере поведения системы. Причем, зачастую, это можно сделать очень простым образом.
Вспомним школьную задачу о падения тела с высоты h. Скорость тела в момент удара о землю можно найти с использованием законов динамики: первого и второго законов Ньютона. Но, эту же задачу можно решить, используя закон сохранения механической энергии, как говорится, в одну строку. Приведем это решение.
Энергия тела до падения определялась его потенциальной энергией 
. После момент ударом о землю его потенциальная энергия полностью перешла в кинетическую и стала равной 
. Поскольку, значение энергии в процессе падения сохранилось, названные можно приравнять и получить скорость тела в момент падения.
.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21