Концепция современного естествознания
.
В разных системах отсчета, двигающихся относительно друг друга время течет по разному, причем в системе отсчета, связанной с объектом наблюдения часы идут медленнее всего, т.е. собственное время всегда минимальное. Собственное время - еще один инвариант преобразований Лоренца, в какой бы инерциальной системе отсчета его ни вычисляли, всегда должен получиться одинаковый результат. Формула (12.3) неоднократно обыгрывалась в фантастических романах, когда отец улетал к звездам на космолете с большой скоростью, возвращался обратно молодым, а его сын, остававшийся на Земле уже успевал состарится.
Обратимся еще раз к примеру, приведенному в параграфе 12.1, в котором рассматривалось взаимодействие двух движущихся зарядов, и ответим на вопрос, почему же все-таки силы взаимодействия окажутся для разных наблюдателей разными. Ответ на него заключается в том, что в движущейся системе отсчета время течет медленнее, и ускорение, а значит, и сила взаимодействия уменьшится.
Кроме изменения хода часов наблюдается изменение размеров (укорочение) быстро движущихся объектов. Этот эффект тоже может быть выведен из преобразований Лоренца. Связь длины отрезка, направленного вдоль скорости движения, в системе К (наблюдаемая длина 
) и в системе K’ (собственная длина 
) задается формулой:
.
Таким образом собственная длина всегда максимальна. Отметим, что сокращаются лишь размеры тела вдоль направления скорости системы K’. Изменение размеров - кажущийся, ненаблюдаемый эффект. Размеры мы определяем, сравнивая длину линейки с размерами тела. Но, и сама линейка в другой системе координат будет менять свои размеры одновременно с телом. Этот эффект напрямую нельзя наблюдать.
Как ни странно, именно сокращение длины и замедление хода времени, предсказанные в теории относительности, удалось наблюдать еще в 30-е годы нашего века. Исследовались нестабильные частицы m-мезоны. Время жизни m-мезонов было измерено, 
. За это время частица могла пролететь расстояние не превышающее 
. Однако, m-мезоны могли рождаться лишь на высоте 20-30 км при столкновении космического излучения с ядрами атомов в атмосфере. Казалось бы, все они должны распасться еще в верхних слоях атмосферы, но приборы на земле уверенно регистрировали их. Объясняется это тем, что рождались они с очень большими скоростями, близкими к скорости света. В соответствии с формулой (12.3) течение времени в их их системе отсчета замедлялось и они успевали пройти расстояние в несколько десятков километров. Но как объяснить это же явление, если наблюдать за частицами в их собственной системе отсчета, ведь в этой системе время жизни частиц составляет действительно . А в этом случае для частиц сокращается длина пройденного ими пути. m-мезоны пролетают десятки километров и достигают земли, но для них в полном соответствии в формулой (12.4) длина этого пути сокращается до нескольких сотен метров. Таким образом, наблюдение одного природного явления подтвердило сразу два, казалось бы, абсурдных следствия из преобразований Лоренца.
В настоящее время существуют очень точные часы, которые показали, что время на движущихся искусственных спутниках Земли отстает от земного времени на 1 секунду за 44 года.
В релятивистской механике предсказан еще целый ряд парадоксальных с точки зрения классической механики явлений. В настоящее время большинство из них наблюдались в экспериментах. При этом не наблюдалось отклонений от предсказаний специальной теории относительности.
12.3 Релятивистская динамика, масса покоя, связь массы и энергии
В параграфе 10.3 обсуждалась инвариантность законов классической механики относительно преобразований Галилея. Преобразования Лоренца связывают не только координаты с координатами, но и время с координатами и наоборот. Естественно, что законы классической механики неинвариантны по отношению к преобразованиям Лоренца. При создании релятивистской механики перед Эйнштейном встал вопрос, как записать второй закон Ньютона, чтобы он был инвариантен относительно преобразований Лоренца. Эйнштейном был получен явный вид основного уравнения динамики в релятивистской форме.
Сначала нужно ввести импульс, который сохранялся бы в любой инерциальной системе отсчета. Традиционный классический импульс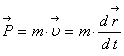 
оказывается неинвариантен по отношению к преобразованиям Лоренца и, как следствие, не сохраняется. Однако, если не меняя формы записи, измерять перемещение 
в лабораторной системе отсчета К, а промежуток времени 
- в системе отсчета K’, связанной с телом, то импульс будет инвариантен к преобразованиям Лоренца и будет сохраняться. Нужно заменить 
на 
. Связь промежутков времени в различных инерциальных системах отсчета задается формулой (12.3). 
.
Здесь mo - классическая масса тела, u - его скорость, измеряемая в лабораторной системе К, а m - релятивистская масса: 
.
Таким образом, импульс тела формально записывается также, как и в классической механике, но понятие массы наполняется новым содержанием. Масса в специальной теории относительности зависит от скорости частицы. Классическую массу частицы mo можно назвать массой покоя. Масса покоя равна массе тела, измеренной в той инерциальной системе отсчета, где тело покоится. Ни в какой системе отсчета масса тела не может быть меньше массы покоя. Масса покоя - еще один инвариант преобразований Лоренца.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21