Учебник по физике для поступающих в ВУЗ
![]()
a = const

При равнозамедленном прямолинейном движении
x = x0 + v0t -
Графиком является парабола
Физический смысл правой части параболы - уменьшение координаты соответствует движению тела в обратном направлении.
Равнопеременное прямолинейное движение – движение с постоянным по модулю и направлению ускорением
![]() = const
= const
Зависимость скорости от времени при равноускоренном и равнозамедленном движении можно рассматривать как частные случаи равнопеременного движения
v x = v0x +axt
Закон равнопеременного движения :
x = x0 + v0xt +
Проекции скоростей и ускорений могут быть как положительными, так и отрицательными.
СВОБОДНОЕ ПАДЕНИЕ ТЕЛ (уч.10кл.стр.52-55)
Определение свободного падения тел. Опыты Галилея, Бойля, Гюйгенса
Ускорение свободного падения (см.ниже уч.10кл.)
Падение тел в воздухе. Сопротивление воздуха.
Свободное падение без начальной скорости. Формулы.
Формулы времени м скорости падения с высоты.
Формулы времени, максимальной высоты при бросании тела вверх с начальной скоростью.
Формулы баллистики. (уч.10кл.стр.61-68)
Все тела независимо от их массы в отсутствии сил сопротивления воздуха падают на землю с одинаковым ускорением, называемым ускорением свободного падения.
Впервые это экспериментально доказал Галилео Галилей. Из-за отсутствия точных часов для измерения малых промежутков времени при падении тел он исследовал скольжение шаров с наклонной плоскости.

При любом угле наклона плоскости расстояние, проходимое шаром, пропорционально квадрату времени движения.
Выводы Галилея были подтверждены англичанином Робертом Бойлем, исследовавшим падение тел в сосуде, из которого был откачан воздух.
Ускорение тел при падении на землю впервые измерил Кристиан Гюйгенс в 1656 г. с помощью маятниковых часов.
Вблизи поверхности Земли g = 9.81 м/с2
Закон свободного падения хорошо наблюдать на луне, где нет атмосферы
При свободном падении без начальной скорости (точка отсчета в точке начала падения)
y = H = gt2/2
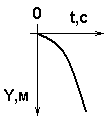
Время падения тела на землю t =
Скорость у земли : vy = gt = g=
В поле силы тяжести тело движется с постоянным ускорением, т.е. равнопеременно, независимо от начальной скорости тела и ее направления
y = y0 + v0yt +
УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ (уч.10кл.стр.52-53)
Свободное падение тел (см. выше)
Величина ускорение свободного падения.
Зависимость ускорения от силы тяжести согласно закону всемирного тяготения
Ускорение тел при падении на землю впервые измерил Кристиан Гюйгенс в 1656 г. с помощью маятниковых часов.
Вблизи поверхности Земли g = 9.81 м/с2
С высотой g изменяется
В поле силы тяжести тело движется с постоянным ускорением, т.е. равнопеременно, независимо от начальной скорости тела и ее направления
y = y0 + v0yt +
БАЛЛИСТИЧЕСКОЕ ДВИЖЕНИЕ(уч.10кл.стр.61-68)
Определение баллистики
Траектория движение в поле силы тяжести
Уравнение баллистического движения
Максимумы графика баллистического движения
Дальность полета при баллистическом движении
Скорость при баллистическом движении
Баллистическое движение при сопротивлении среды
Баллистика – раздел механики, изучающий движение тел в поле тяжести земли.
Основные допущения при рассмотрении баллистического движения:
- тело – материальная точка
- движение тела рассматривается вблизи поверхности Земли, когда высота подъема тела мала по сравнению с радиусом Земли
- сопротивление воздуха не учитывается
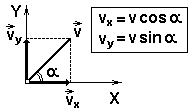
В Евклидовом физическом пространстве перемещение тела по координатным осям X и Y можно рассматривать независимо.
Криволинейное баллистическое движение можно рассматривать как результат сложения двух прямолинейных движений: равномерного движения по оси X и равнопеременного по оси Y (под действием ускорения g)
Закон баллистического движения в координатной форме:
 Þ y = x tg(α) -
Þ y = x tg(α) -

Графиком баллистического движения в поле силы тяжести является парабола, проходящая через начало координат.
Время подъема на максимальную высоту (максимум функции y(t)):
tmax = =
Максимальная высота подъема:
ymax = y(tmax) =
Максимальная дальность полета ( учитывая симметричность параболы и что 2sin(α)cos(α)=sin(2α)):
xmax = x(2tmax) =
Дальность полета при одной и той же начальной скорости зависит от угла, под которым тело брошено к горизонту.
Максимальное значение синуса будет при угле 2α = 90о, следовательно максимальная дальность полета будет при угле: α = 45о
В отсутствии сопротивления воздуха максимальная дальность полета тела в поле силы тяжести достигается при вылете под углом 45о к горизонту.
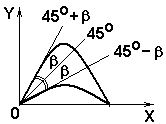
При α = 45о + β – навесная траектория
При α = 45о - β – настильная траектория
Дальность полета при этом одинаковая

Для расчета скорости в произвольной точке траектории (направлена по касательной к траектории), и для определения угла β, который образует вектор скорости в горизонтом, достаточно знать проекции скорости на оси X и Y:
v = (по теореме Пифагора из треугольника скоростей)
tg (β) =
При равномерном движении по оси X проекция скорости остается постоянной:
vx = v0 cos(α)
По оси Y действует ускорение g:
vy = v0 sin(α) - gt
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
