Учебник по физике для поступающих в ВУЗ
Ответ на вопрос, какая физическая величина является однозначным показателем наличия внешнего воздействия, был дан Ньютоном во втором законе (см.ниже)
Инерциальная система отсчета – Система отсчета, в которой законы Ньютона выполняются без дополнений или ограничений
Явление сохранения скорости тела при отсутствии внешних воздействий называется инерцией.
Первый закон Ньютона выполняется не во всех системах отсчета.
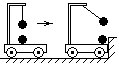
Сначала тележка движется прямолинейно и равномерно относительно земли. На ней находятся два шарика. Один лежит на горизонтальной поверхности тележки, а другой подвешен на нити.
Силы, действующие на каждый шарик по вертикали, уравновешены, по горизонтали никакие силы на них не действуют.
Шарики будут находится в покое относительно тележки при любой скорости ее движения относительно земли – главное, чтобы эта скорость была постоянна.
При торможении тележки оба шарика приходят в движение, т.е. меняют свою скорость относительно тележки, хотя никакие силы на них по прежнему не действуют.
Значит, в системе отсчета, связанной с тележкой, тормозящей относительно земли, закон инерции не выполняется.
Поэтому с точки зрения современных представлений первый закон Ньютона формулируется так:
Существуют такие системы отсчета, относительно которых тела сохраняет свою скорость неизменной, если на них не действуют другие тела.
Следует помнить, что в первом законе Ньютона речь идет о телах, которые могут быть приняты за материальную точку.
Те системы отсчета, в которых закон инерции выполняется, называются инерциальными, а те, в которых не выполняется – неинерциальными.
ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА (уч.10кл.стр.83-86)
Инерция (см.выше) Краткое определение.
Инерциальные системы отсчета. Определение
Отличие инерциальных систем от неинерциальных
Относительность покоя и движение в различных системах отсчета. Примеры
Преобразования Галилея
Время в системах отсчета
Принцип относительности Галилея и его физический смысл
Свойства инерциальных систем отсчета
Системы отсчета, относительно которых тела при отсутствии внешних воздействий движутся прямолинейно и равномерно, называются инерциальными системами отсчета. Системы отсчета, связанные с землей считают инерциальными, при условии пренебрежения вращением земли.
Причиной изменения скорости тела всегда является его взаимодействие с другими телами. При взаимодействии двух тел всегда изменяются скорости, т.е. приобретаются ускорения. Отношение ускорений двух тел одинаково при любых взаимодействиях.
Свойство тела, от которого зависит его ускорение при взаимодействии с другими телами, называется инертностью.
Количественной мерой инертности является масса тела
Явление сохранения скорости тела при отсутствии внешних воздействий называется инерцией.
Движение по инерции – движение происходящее без внешних воздействий
(В земных условиях практически не встречается)
Принцип инерции Галилея:
Если на тело не действуют внешние силы, то оно сохраняет состояние покоя или равномерного прямолинейного движения
Принцип инерции сформулирован Галилеем при изучении движения тел при максимальном уменьшении сил трения.
Понятия «движение» и «покой» относительны и зависят от выбора системы отсчета.
Инерциальная система отсчета – система отсчета, в которой тело, не взаимодействуя с другими телами, сохраняет состояние покоя или равномерного прямолинейного движения.
Инерциальные системы отсчета – покоящиеся или движущиеся равномерно и прямолинейно относительно друг друга
В инерциальных системах отсчета состояния покоя и равномерного прямолинейного движения эквивалентны и взаимозаменяемы
Системы отсчета, в которых принцип инерции не выполняется, называют неинерциальными
Пример неинерциальной системы – автобус, трогающийся с места с ускорением. Пассажиров отбрасывает назад, в сторону противоположную движению, при отсутствии внешних сил.
Инерциальными модно считать так же системы отсчета, связанные с любым телом, которое покоится или движется равномерно и прямолинейно относительно поверхности земли.
Системы, движущиеся относительно инерциальных с ускорением, являются неинерциальными.
Преобразования Галилея - показывают, как связаны между собой координаты и скорость тела в различных инерциальных системах отсчета

За время t платформа сместиться относительно столба на vt
Автомобиль проедет по платформе расстояние x’= vxt
и будет находится от столба на расстоянии x = x’ + vt
Координаты тела (автомобиля) в различных системах отсчета X и X’ связывают преобразования Галилея:
x’ = x –vt
vx = x/t
Закон сложения скоростей:
скорость движения материальной точки по отношению к системе отсчета, принимаемой за неподвижную, равна векторной сумме скоростей движения точки в подвижной системе и скорости движения подвижной системы относительно неподвижной:
![]()
vx = vx’ + v
Движение инерциальной системы отсчета не оказывает влияния на прямолинейное равномерное движение тела или его состояние покоя в этой системе
Преобразование Галилея справедливо, если v<<с = 3*108м/с.
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
Во всех инерциальных системах отсчета законы классической механики имеют один и тот же вид
Это означает, что при переходе от одной инерциальной системы отсчета к другой все математические формулы, описывающие законы механики, не меняются.
Время в классической механике является абсолютным: оно едино во всех инерциальных системах отсчета. Движущиеся и неподвижные часы идут одинаково.
ВЗАИМОДЕЙСТВИЕ ТЕЛ (уч.10кл.стр.89-92)
Сила как мера взаимодействия тел
Связи силы и ускорения(см.ниже уч.10кл.стр.89-92)
Второй закон Ньютона (см.ниже уч.10кл.стр.89-92)
При одновременном действии на одно тело нескольких сил тело движется с ускорением, являющимся векторной суммой ускорений, которые возникли бы при воздействии каждой из этих сил в отдельности.
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
