Учебник по физике для поступающих в ВУЗ
В верхней точке траектории вертикальная составляющая компонента скорости равна нулю.
Сопротивление воздуха по мере увеличения скорости растет не линейно. Сначала пропорционально , потом примерно в квадрате от скорости, потом в кубе. Точный расчет достаточно громоздок.

КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ ТОЧКИ НА ПРИМЕРЕ ДВИЖЕНИЯ ПО ОКРУЖНОСТИ С ПОСТОЯННОЙ ПО МОДУЛЮ СКОРОСТЬЮ (уч.10кл.стр.70-73)
Периодическое движение. Определение и примеры
Определение периода и частоты
Движение по окружности как пример периодического движения
Определение равномерного движения тела по окружности
Определение и формулы периода и частоты при равномерном движении по окружности
Фаза вращения и угловая скорость.
Определение угловой скорости и единицы измерения. Радиан, градус, оборот.
Период вращения через угловую скорость. Формула
Линейная скорость и ее вектор при движении по окружности. Формула. Зависимость от радиуса вращения.
Периодическое движение – движение, повторяющееся через равные промежутки времени.
Период – минимальный интервал времени, через который движение повторяется
Обозначение Т. Единица измерения – с
Различают два вида периодического движения:
- вращательное
- колебательное
Движение абсолютно твердого тела (не деформирующегося при движении и взаимодействии), при котором все его точки в данный момент времени движутся в одном направлении по плоскости или пространственной замкнутой траектории одинаково, называется поступательным движением.
Для его описания необходимо и достаточно описать движение одной точки тела.
Движение, при котором траектории всех точек тела являются окружностями с центром на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением.
Колебательное движение – движение вдоль одного и того же отрезка с изменением направления движения
При равномерном движении тела по окружности модуль скорости тела остается постоянным.
Если размерами тела можно пренебречь по сравнению с радиусом окружности, то тело можно рассматривать, как материальную точку.
 2π (радиан) = 360о – один полный оборот
2π (радиан) = 360о – один полный оборот
Положение тела в пространстве можно описать тремя способами:
- с помощью пути, пройденного от начальной точка А до точки В
Время одного полного оборота по окружности
T =
Период вращения – время одного полного оборота по окружности
- с помощью угла поворота радиус-вектора относительно его начального положения
Фаза вращения α – угол поворота радиуса-вектора в произвольный момент времени относительно его начального положения
Угол поворота в единицу времени характеризует угловую скорость
Угловая скорость – физическая величина, равная отношению угла поворота тела к промежутку времени, в течении которого этот поворот произошел.
ω =
Единицы измерения = 1 рад/с (при измерении угла поворота в радианах)
Один полный оборот 360o = 2π радиан
При равномерном вращении по окружности угловая скорость всех точек тела одинакова, и характеризует движения вращающегося тела в целом.
Период вращения – время одного оборота:
T =
Частота вращения – число оборотов в единицу времени:
ν =
Единица измерения – с-1=1/с
ω = = 2πν
Линейная скорость при движении по окружности:
v = ωr = r = 2πνr
Линейная скорость растет пропорционально расстоянию r от оси вращения.
За промежуток времени t радиус-вектор поворачивается на угол α = ωt

Координаты меняются по законам синуса и косинуса
x = r cos(ωt)
y = r sin(ωt)
В случае равномерного вращения скорость меняется только по направлению
Нормальное ускорение an =![]()
(математический смысл an = – производная скорости по времени)
при Dt→0 Dv→v (вектора v1 и v2 сближаются) и an = ; φ =
Угловое ускорение: E – векторная величина
E =
Единица измерения - рад/c2
В общем случае уравнения вращательного движения:
v(t) = v0 + at
r(t) = r0 + v0t +
φ(t) = ω0t +
ω(t) = ω0 + Et
Угловая скорость характеризует быстроту вращения
ω = (производная углового перемещения по времени)
Угловое перемещение Dj – векторная величина, равная углу поворота радиус-вектора (Dr = r2 - r1) и направленная перпендикулярно плоскости вращения по правилу винта
Единица измерения - рад
Связь между линейной и угловой скоростью:
v = ωr
Принцип независимости движений рассматривает движение любой точки тела как сумму двух движений – поступательного и вращательного:
![]()
ЦЕНТРОСТРЕМИТЕЛЬНОЕ УСКОРЕНИЕ (уч.10кл.стр.70-73)
Вектор линейной скорости при движении по окружности и его изменение.
Природа возникновения центростремительного ускорения
Ускорение как изменение вектора скорости.
Ускорение как производная изменения скорости по времени.
Направление вектора центростремительного ускорения.
Вывод формулы центростремительного ускорения
Нормальное и тангенциальное ускорения при движении по окружности
Использование формул движения по окружности при криволинейном движении тела
Скорость тела –векторная величина. Любое изменение скорости во времени означает появление ускорения. При этом может меняться не только величина, но и вектор скорости.
Если меняется только модуль скорости – прямолинейное ускоренное движение
Если меняется только направление вектора скорости – равномерное криволинейное движение
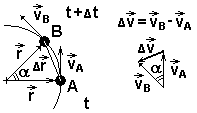
из подобия треугольников = Þ ∆v = ∆r
Мгновенное (нормальное) ускорение
Перейти на страницу: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
